
【题目】【倾听理解】(这是习题讲评课上师生围绕一道习题的对话片断)
如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与A、B重合),OD⊥BC,OE⊥AC,垂足分别为D、E.

师:当BD=1时,同学们能求哪些量呢?
生1:求BC、OD的长.
生2:求![]() 、
、![]() 的长.
的长.
……
师:正确!老师还想追问的是:去掉“BD=1”,大家能提出怎样的问题呢?
生3:求证:DE的长为定值.
生4:连接AB,求△ABC面积的最大值.
……
师:你们设计的问题真精彩,解法也很好!
【一起参与】
(1)求“生2”的问题:“当BD=1时,求![]() 、
、![]() 的长”;
的长”;
(2)选择“生3”或“生4”提出的一个问题,并给出解答.
【答案】(1)![]() 的长为
的长为![]() π;(2)
π;(2)![]() 的长为
的长为![]() π;(2)见解析
π;(2)见解析
【解析】试题分析:
(1)如图:
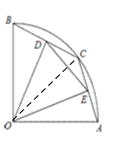
连接OC,当BD=1时,由“垂径定理”可得BC=2,从而可证△OBC为等边三角形,得到∠BOC=60°,∠AOC=30°,就可以由弧长公式求两条弧的长了;
(2)①“生3的问题”,如图:
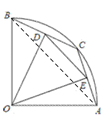
连接AB,在Rt△AOB中,由已知易得![]() ,由已知和“垂径定理”可得D、E分别是BC和AC的中点,从而可得DE是△OAB的中位线,由“三角形中位线定理”可得DE=
,由已知和“垂径定理”可得D、E分别是BC和AC的中点,从而可得DE是△OAB的中位线,由“三角形中位线定理”可得DE=![]() AB=
AB=![]() ;
;
②“生4的问题”,如图:

由①可知, ![]() ,OC=2,当点C为
,OC=2,当点C为![]() 的中点时,OC⊥AB,此时OF最短为
的中点时,OC⊥AB,此时OF最短为![]() ,CF最长为
,CF最长为![]() ,△ABC面积最大;
,△ABC面积最大;
试题解析:
(1)连OC,当BD=1时,
∵OD⊥BC
∴BC=2BD=2,∴△OBC是等边三角形.∴∠BOC=60°,∴∠AOC=30°,
∴![]() 的长为
的长为![]() ,
, ![]() 的长为
的长为![]() .
.
(2)生3的问题:连结AB,在Rt△AOB中,AB=![]() ,
,
∴DE=![]() AB=
AB=![]() .
.
生4的问题:∵当点C为
∴ 当点C为![]() 中点时,CF最长,由AB=
中点时,CF最长,由AB=![]() 是定值,可知此时,△ABC面积最大,
是定值,可知此时,△ABC面积最大,
∵OC⊥AB,
∴OF=![]() AB=
AB=![]() ,
,
∴CF=2-![]() ,
,
∴S△ABC最大=![]() .
.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】在不透明的箱子中,装有红、白、黑各一个球,它们除了颜色之外,没有其他区别。
(1)随机地从箱子里取出一个球,则取出红球的概率是多少?
(2)随机地从箱子里取出1个球,然后放回,再摇匀取出第二个球,请你用画树状图或列表的方法表示所有等可能的结果,并求两次取出相同颜色球的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是直径,点D是⊙O上的一点,点C是![]() 的中点,弦CM垂直AB于点F,连接AD,交CF于点P,连接BC,∠DAB=30°
的中点,弦CM垂直AB于点F,连接AD,交CF于点P,连接BC,∠DAB=30°
(1)求∠ABC的度数;
(2)若CM=8![]() ,求
,求![]() 的长度.(结果保留π)
的长度.(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校就“遇见路人摔倒后如何处理”的问题,随机抽取该校部分学生进行问卷调查,图1和图2是整理数据后绘制的两幅不完整的统计图. 请根据图中提供的信息,解答下列问题:
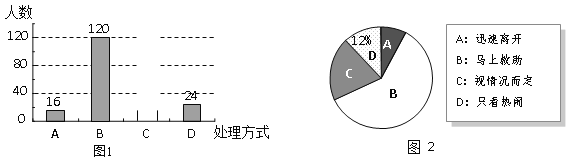
(1)该校随机抽查了 名学生?请将图1补充完整;
(2)在图2中,“视情况而定”部分所占的圆心角是 度;
(3)在这次调查中,甲、乙、丙、丁四名学生都选择“马上救助”,现准备从这四人中随机抽取两人进行座谈,试用列表或树形图的方法求抽取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“不闯红灯,珍惜生命”活动中,文明中学的关欣和李好两位同学某天来到城区中心的十字路口,观察、统计上午7:00~12: 00中闯红灯的人次,制作了两个数据统计图(图20-3-4).
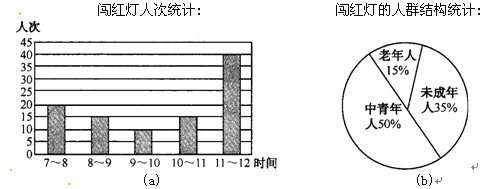
(1)求图a提供的五个数据(各时段闯红灯人次)的众数和平均数.
(2)估计一个月(按30天计算)上午7:00~12:00在该十字路口闯红灯的未成年人约有_____人次.
(3)根据统计图提供的信息向交通管理部门提出一条合理化建议
查看答案和解析>>
科目:初中数学 来源: 题型:
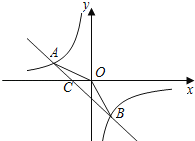
【题目】如图,在平面直角坐标系xOy中,若点A(﹣2,n),B(1,﹣2)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标;
(3)求点O到直线AB的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com