
【题目】如图,在⊙O中,AB是直径,点D是⊙O上的一点,点C是![]() 的中点,弦CM垂直AB于点F,连接AD,交CF于点P,连接BC,∠DAB=30°
的中点,弦CM垂直AB于点F,连接AD,交CF于点P,连接BC,∠DAB=30°
(1)求∠ABC的度数;
(2)若CM=8![]() ,求
,求![]() 的长度.(结果保留π)
的长度.(结果保留π)

【答案】(1)30°;(2)![]()
【解析】试题分析:
(1)如图,

连接BD,由点C是![]() 的中点,易得∠ABC=
的中点,易得∠ABC=![]() ∠ABD,而BD是圆的直径可得△ABD是直角三角形,再由∠A=30°就可求得∠ABD,从而求得∠ABC;
∠ABD,而BD是圆的直径可得△ABD是直角三角形,再由∠A=30°就可求得∠ABD,从而求得∠ABC;
(2)连接OC,由(1)中结论易得∠AOC=60°,所以我们只需在Rt△OFC中,利用垂径定理求得CF,再利用“直角三角形中30°的角所对直角边等于斜边的一半”和“勾股定理”可求得OC,最后用“弧长公式”求![]() 的长;
的长;
试题解析:
(1)连接BD,∵AB为⊙O的直径,
∴∠ADB=90°,
∵∠DAB=30°,
∴∠ABD=90°-30°=60°,
∵C是![]() 的中点,
的中点,
∴∠ABC=∠DBC=![]() ∠ABD=30°;
∠ABD=30°;
(2)连接OC,则∠AOC=2∠ABC=60°,
∵CM⊥直径AB于点F,
∴CF=![]() CM=
CM=![]() ,∠CFO=90°,
,∠CFO=90°,
∴在Rt△COF中,∠OCF=30°,
∴OC=2OF,OF2+CF2=OC2,即![]() ,
,
解得:OF=4,∴OC=8,
∴![]() 的长度为
的长度为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2﹣(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴分别交于D、E两点.
(1)求m的值;
(2)求A、B两点的坐标;
(3)当﹣3<x<1时,在抛物线上是否存在一点P,使得△PAB的面积是△ABC面积的2倍?若存在,请求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核,三人各项得分如表:
笔试 | 面试 | 体能 | |
甲 | 84 | 78 | 90 |
乙 | 85 | 80 | 75 |
丙 | 80 | 90 | 73 |
![]() 根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
![]() 该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按
该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按![]() 的比例计入总分
的比例计入总分![]() 根据规定,请你说明谁将被录用.
根据规定,请你说明谁将被录用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【倾听理解】(这是习题讲评课上师生围绕一道习题的对话片断)
如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与A、B重合),OD⊥BC,OE⊥AC,垂足分别为D、E.

师:当BD=1时,同学们能求哪些量呢?
生1:求BC、OD的长.
生2:求![]() 、
、![]() 的长.
的长.
……
师:正确!老师还想追问的是:去掉“BD=1”,大家能提出怎样的问题呢?
生3:求证:DE的长为定值.
生4:连接AB,求△ABC面积的最大值.
……
师:你们设计的问题真精彩,解法也很好!
【一起参与】
(1)求“生2”的问题:“当BD=1时,求![]() 、
、![]() 的长”;
的长”;
(2)选择“生3”或“生4”提出的一个问题,并给出解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
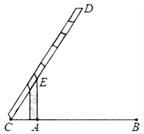
【题目】如图,王刚在研究性学习活动中,对自己家所在的小区进行调查后发现,小区汽车入口宽AB为3.2m,在入口的一侧安装了停止杆CD,其中AE为支架.当停止杆仰起并与地面成60°角时,停止杆的端点C恰好与地面接触,此时CA为0.7m.在此状态下,若一辆货车高3m,宽2.5m,入口两侧不能通车,那么这辆货车在不碰杆的情况下,能从入口内通过吗?请你通过计算说明.(参考数据: ![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0; ②b>a+c;③9a+3b+c>0;④c<-3a;⑤a+b+c≥m(am+b)+c,其中正确的有( )个。
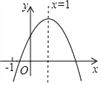
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形错误的是( )
A. a-c>b-c,则a>bB. 2a<2b,则a<b
C. -a-c>-b-c,则a>bD. -2a<-2b,则a>b
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com