
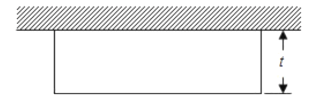
【题目】有长为l的篱笆,利用它和房屋的一面墙围成如图形状的园子,园子的宽为t.
(1)用关于l,t的代数式表示园子的面积;这个代数式是多项式还是单项式?
(2)若l=100固定不变,若t的值取20,25,30时,则哪一种取法所围成的园子面积最大?
【答案】(1)面积为tl-2t2; 是多项式.(2)当t取25时围成的园子面积最大
【解析】
(1)因为篱笆的长为l,当宽为t时,根据图形可知园子的长为l﹣2t,那么根据长方形的面积公式可知面积为t(l﹣2t);观察即可得出是多项式
(2)分别求出t的值取20,25,30时,园子面积,比较面积即可.
解:(1)由题意可知:篱笆的长为l,当宽为t时,园子的长为l﹣2t,则面积为t(l﹣2t)=![]() ,可知这个式子是多项式;
,可知这个式子是多项式;
(2)l=100,当t=20时,t(l﹣2t)=20×(100﹣2×20)=1200;
l=100,当t=25时,t(l﹣2t)=25×(100﹣2×25)=1250;
l=100,当t=30时,t(l﹣2t)=30×(100﹣2×30)=1200;
∴当t取25时围成的园子面积最大.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某学校计划在总费用![]() 元的限额内,租用汽车送
元的限额内,租用汽车送![]() 名学生和
名学生和![]() 名教师集体参加校外实践活动,为确保安全,每辆汽车上至少要有
名教师集体参加校外实践活动,为确保安全,每辆汽车上至少要有![]() 名教师.现有甲、乙两种大客车,它们的载客量和租金如下表所示.
名教师.现有甲、乙两种大客车,它们的载客量和租金如下表所示.
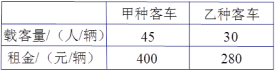
(1)根据题干所提供的信息,确定共需租用多少辆汽车?
(2)请你给学校选择一种最节省费用的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AB=DC,AC与BD相交于P.已知A(4,6),B(2,2),D(8,6),则点P的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一条不完整的数轴上从左到右有点A,B,C,其中AB=2BC,设点A,B,C所对应数的和是m.
(1)若点C为原点,BC=1,则点A,B所对应的数分别为 , ,m的值为 ;
(2)若点B为原点,AC=6,求m的值.
(3)若原点O到点C的距离为8,且OC=AB,求m的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
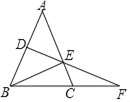
【题目】如图,在△ABC中,点D是AB的中点,点F是BC延长线上一点,连接DF,交AC于点E,连接BE,∠A=∠ABE.
(1)求证:DF是线段AB的垂直平分线;
(2)当AB=AC,∠A=46°时,求∠EBC及∠F的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
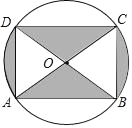
【题目】如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A、B、C、D,得到四边形ABCD,若AC=10cm,∠BAC=36°,则图中阴影部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
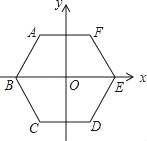
【题目】如图,边长为4的正六边形ABCDEF的中心与坐标原点O重合,AF∥x轴,将正六边形ABCDEF绕原点O顺时针旋转n次,每次旋转60°,当n=2018时,顶点A的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
元且期间,我市各大商场掀起购物狂湖,现有甲、乙、丙三个商场开展的促销活动如表所示:
商场 | 优惠活动 |
甲 | 全场按标价的 |
乙 | 实行“满 (如:顾客购衣服 |
丙 | 实行“满 |
根据以上活动信息,解决以下问题:
(1)三个 商场同时出售一件标价![]() 元的上衣和一条标价
元的上衣和一条标价![]() 元的裤子,王阿姨想买这一套衣服,她应该选择哪家商场更划算?
元的裤子,王阿姨想买这一套衣服,她应该选择哪家商场更划算?
(2)黄 先生发现在甲、乙商场同时出售一件标价![]() 元的上衣和一条标价
元的上衣和一条标价![]() 多元的裤子,最后付款也一样,诸问这条裤子的标价是多少元?
多元的裤子,最后付款也一样,诸问这条裤子的标价是多少元?
(3)丙商场又推出 “先打折”,“再满![]() 减
减![]() 元”的活动,张先生买了一件标价为
元”的活动,张先生买了一件标价为![]() 元的上衣,张先生发现竟然比没打折前多付了
元的上衣,张先生发现竟然比没打折前多付了![]() 元钱,问丙商场先打了多少折后再参加活动?
元钱,问丙商场先打了多少折后再参加活动?
查看答案和解析>>
科目:初中数学 来源: 题型:
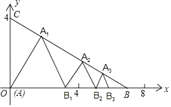
【题目】如图,已知,点A(0,0)、B(4![]() ,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…则第2017个等边三角形的边长等于( )
,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…则第2017个等边三角形的边长等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com