
| ְ�� | �� | �� |
| �����ۼ��������� | 100 | 80 |
| �¹��ʣ�Ԫ�� | 4500 | 4100 |
���� ��Ա�����»�������ΪxԪ������ÿ����Ʒ�Ľ������ΪyԪ������ͼ���ɵã�����100�����¹���Ϊ4500Ԫ������80�����¹���Ϊ4100Ԫ���ݴ��з�������⣮
��� �⣺��Ա�����»�������ΪxԪ������ÿ����Ʒ�Ľ������ΪyԪ��
������ã�$\left\{\begin{array}{l}{x+100y=4599}\\{x+80y=4100}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=2500}\\{y=20}\end{array}\right.$��
��Ա�����»�������Ϊ2500Ԫ������ÿ����Ʒ�Ľ������Ϊ20Ԫ��
���� ���⿼���˶�Ԫһ�η������Ӧ�ã������Ĺؼ��Ƕ������⣬���δ֪�����ҳ����ʵĵ�����ϵ���з�������⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6 | B�� | 7 | C�� | 8 | D�� | 9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
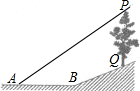 ��֪����ͼ��б��BQ�¶�i=5��12����ΪQC��BC�ij���֮�ȣ�����б��BQ����һ��������PQ��������A�����������P������Ϊ�������Ҳ��ˮƽ��AB=8�ף�����BQ=13�ף�tan��=0.75����A��B��P��Q��ͬһƽ���ϣ�PQ��AB�ڵ�C����������PQ�ĸ߶ȣ�
��֪����ͼ��б��BQ�¶�i=5��12����ΪQC��BC�ij���֮�ȣ�����б��BQ����һ��������PQ��������A�����������P������Ϊ�������Ҳ��ˮƽ��AB=8�ף�����BQ=13�ף�tan��=0.75����A��B��P��Q��ͬһƽ���ϣ�PQ��AB�ڵ�C����������PQ�ĸ߶ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| X | �� | -2 | -1 | 0 | 1 | 2 | �� |
| y | �� | 4 | 0 | -2 | -2 | 0 | �� |
| A�� | �������� | B�� | ��-1��x��2ʱ��y��0 | ||
| C�� | ͼ��ĶԳ�����ֱ��x=$\frac{1}{2}$ | D�� | ������Сֵ��-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
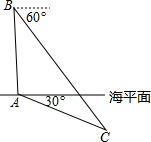 �й������˹�����������ںں�����������ϰ������ϰ���Ҿ���A���DZͧC�ĸ���Ϊ30�㣬λ�ھ���A���Ϸ�1600�ķ�DZֱ����B���DZͧC�ĸ���Ϊ60�㣬�Ը��������������DZͧC�뺣ƽ�����DZ��ȣ�
�й������˹�����������ںں�����������ϰ������ϰ���Ҿ���A���DZͧC�ĸ���Ϊ30�㣬λ�ھ���A���Ϸ�1600�ķ�DZֱ����B���DZͧC�ĸ���Ϊ60�㣬�Ը��������������DZͧC�뺣ƽ�����DZ��ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 165 | B�� | 168 | C�� | 170 | D�� | 172 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com