
 如图,在平面直角坐标系中,一块等腰直角三角形ABC的直角顶点A在y轴上,坐标为(0,-1),另一顶点B坐标为(-2,0),已知二次函数y=$\frac{3}{2}$x2+bx+c的图象经过B,C两点,过点C作CD⊥y轴,垂足为点D
如图,在平面直角坐标系中,一块等腰直角三角形ABC的直角顶点A在y轴上,坐标为(0,-1),另一顶点B坐标为(-2,0),已知二次函数y=$\frac{3}{2}$x2+bx+c的图象经过B,C两点,过点C作CD⊥y轴,垂足为点D分析 (1)证△AOB≌△CDA即可;
(2)求出C点坐标,再用待定系数法求解即可;
(3)设出M点的横坐标,纵坐标用横坐标表示,N点的纵坐标也用M的横坐标表示,将MN的长度表示为M、N两点的纵坐标之差,也就是将MN表示成M点横坐标的二次函数,通过配方求出最大值;
(3)由BP⊥PC,说明A、B、C、P四点共圆,又由于直尺移动到抛物线对称轴处,说明P点就是三角形ABC外接圆与抛物线对称轴的交点,作出图形,利用相似三角形的线段比例求解P点坐标,∠CPA的度数由圆周角性质直接写出.
解答 解:(1)∵∠CAB=90°,
∴∠CAD+∠BAO=90°,
∵∠BAO+∠ABO=90°,
∴∠ABO=∠CAD,
在△AOB和△CDA中,
$\left\{\begin{array}{l}{∠ABO=∠CAD}\\{∠ADC=∠BOA}\\{AB=CA}\end{array}\right.$,
∴△AOB≌△CDA(AAS)
∴AO=CD,AD=BO;
(2)∵AO=CD,AD=BO,A(0,-1),B(-2,0),
∴C(-1,-3),
将B、C两点的坐标代入y=$\frac{3}{2}$x2+bx+c得:$\left\{\begin{array}{l}{-3=\frac{3}{2}-b+c}\\{0=6-2b+c}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=\frac{3}{2}}\\{c=-3}\end{array}\right.$,
∴$y=\frac{3}{2}{x}^{2}+\frac{3}{2}x-3$;
(3)∵B(-2,0),C(-1,-3),
∴直线BC的解析式为:y=-3x-6,
设M(m,-3m-6),则N(m,$\frac{3}{2}{m}^{2}+\frac{3}{2}m-3$),
∴MN=$-3m-6-\frac{3}{2}{m}^{2}-\frac{3}{2}m+3$=$-\frac{3}{2}{m}^{2}-\frac{9}{2}m-3$=$-\frac{3}{2}{(m+\frac{3}{2})}^{2}+\frac{3}{8}$,
∴当m=-$\frac{3}{2}$时,MN取最大值$\frac{3}{8}$;
(4)∵BP⊥PC,∴∠BPC=90°=∠BAC,
∴A、B、C、P四点共圆,
即点P是△ABC外接圆与抛物线对称轴的交点,如图,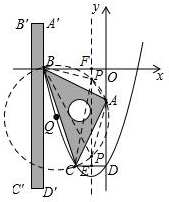
设抛物线对称轴与CD交于点E,与x轴交于点F,则E(-$\frac{1}{2}$,-3),F(-$\frac{1}{2}$,0),
∵BP⊥CP,
∴∠CPE+∠BPF=90°,
∵∠PBF+∠BPF=90°,
∴∠CPE=∠PBF,
∴△PBF∽△CPE,
∴$\frac{BF}{PF}=\frac{PE}{CE}$,
设PF=t,则PE=3-t,
∴$t(3-t)=\frac{3}{2}×\frac{1}{2}$,
解得:t=$\frac{3-\sqrt{6}}{2}$或t=$\frac{3+\sqrt{6}}{2}$,
∴P点坐标为(-$\frac{1}{2}$,$-\frac{3-\sqrt{6}}{2}$)或(-$\frac{1}{2}$,$-\frac{3+\sqrt{6}}{2}$),
当P点坐标为(-$\frac{1}{2}$,$-\frac{3-\sqrt{6}}{2}$)时,∠CPA=∠ABC=45°,
当P点坐标为(-$\frac{1}{2}$,$-\frac{3+\sqrt{6}}{2}$)时,∠CPA=180-∠ABC=135°.
点评 本题考查了全等三角形的判定与性质、待定系数法求二次函数的解析式、配方法求二次函数最值、相似三角形的判定与性质、四点共圆的判定与性质、圆周角的性质等多个知识点,有一定综合性,难度中等.判断出A、B、C、P四点共圆是解决第(4)问的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
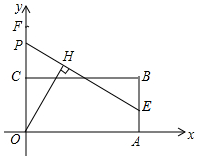 如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(7,3),点E在边AB上,且AE=1,已知点P为y轴上一动点,连接EP,过点O作直线EP的垂线段,垂足为点H,在点P从点F(0,$\frac{25}{4}$)运动到原点O的过程中,点H的运动路径长为$\frac{5\sqrt{2}π}{4}$.
如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(7,3),点E在边AB上,且AE=1,已知点P为y轴上一动点,连接EP,过点O作直线EP的垂线段,垂足为点H,在点P从点F(0,$\frac{25}{4}$)运动到原点O的过程中,点H的运动路径长为$\frac{5\sqrt{2}π}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示的是一个三棱柱,用一个平面先后三次截这个三棱柱.
如图所示的是一个三棱柱,用一个平面先后三次截这个三棱柱.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com