
����Ŀ����֪������![]() �Ķ���Ϊ��D������x���ཻ��A��B���㣨��A�ڵ�B����ࣩ����y���ཻ�ڵ�C��
�Ķ���Ϊ��D������x���ཻ��A��B���㣨��A�ڵ�B����ࣩ����y���ཻ�ڵ�C��

��1�����A��B��C��D�����ꣻ
��2����y������������Ƿ���ڵ�P��ʹ�Ե�P��O��AΪ���������������AOC���ƣ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
��3��ȡ��E��![]() ��0���͵�F��0��
��0���͵�F��0��![]() ����ֱ��l����E��F���㣬��G���߶�BD���е㣮
����ֱ��l����E��F���㣬��G���߶�BD���е㣮
����G�Ƿ���ֱ��l�ϣ���˵�����ɣ�
�������������Ƿ���ڵ�M��ʹ��M����ֱ��l�ĶԳƵ���x���ϣ������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
���𰸡��⣺��1�� D��![]() ����4��
����4��
��2�� P��0��![]() ����0��
����0��![]() ��
��
��3���������
��������
��1����y=0�������x��һԪ���η������A��B�����꣬��x=0�����C�����꣬�ٸ��ݶ������깫ʽ���㼴���������D�����ꡣ
��2�����ݵ�A��C���������OA��OC�ij����ٷ�OA��OA�Ƕ�Ӧ�ߣ�OA��OC�Ƕ�Ӧ������������������������ζ�Ӧ�߳ɱ�����ʽ���OP�ij����Ӷ��ý⡣
��3������ֱ��l�Ľ���ʽΪy=kx+b��k��0�������ô���ϵ������һ�κ�������ʽ���ֱ��l�Ľ���ʽ���������е㹫ʽ�����G�����꣬Ȼ�����ֱ���ϵ������������֤���ɡ�
���������ߵĶԳ�����x�ύ��ΪH�����OE��OF��HD��HB�ij���Ȼ�������OEF����HDB���ƣ��������������ζ�Ӧ����������OFE=��HBD��Ȼ�����EG��BD���Ӷ��õ�ֱ��l���߶�BD�Ĵ�ֱƽ���ߣ������߶δ�ֱƽ���ߵ����ʵ�D����ֱ��l�ĶԳƵ����B���Ӷ��жϳ���M����ֱ��DE�������ߵĽ��㡣����ֱ��DE�Ľ���ʽΪy=mx+n�����ô���ϵ������һ�κ����������ֱ��DE�Ľ���ʽ��Ȼ���������߽���ʽ������⼴�ɵõ����������ĵ�M��
�⣺��1����![]() �У���y=0����
�У���y=0����![]() �������ã�4x2��12x��7=0��
�������ã�4x2��12x��7=0��
���x1=![]() ��x2=
��x2=![]() ����A��
����A��![]() ��0����B��
��0����B��![]() ��0����
��0����
��![]() ����x=0����y=
����x=0����y=![]() ����C��0��
����C��0��![]() ����
����
��![]() ��������D��
��������D��![]() ����4����
����4����
��2����y���������ϴ��ڷ��������ĵ�P��
���P��������0��y����
��A��![]() ��0����C��0��
��0����C��0��![]() ������OA=
������OA=![]() ��OC=
��OC=![]() ��OP=y��
��OP=y��
����OA��OA�Ƕ�Ӧ�ߣ�����AOP�ס�AOC����![]() ����y=OC=
����y=OC=![]() ����ʱ��P��0��
����ʱ��P��0��![]() ����
����
����OA��OC�Ƕ�Ӧ�ߣ�����POA�ס�AOC����![]() ����
����![]() ��
��
���y=![]() ����ʱ��P��0��
����ʱ��P��0��![]() ����
����
�������������������ĵ�P��������P��0��![]() ����0��
����0��![]() ����
����
��3������ֱ��l�Ľ���ʽΪy=kx+b��k��0����
��ֱ��l������E��![]() ��0���͵�F��0��
��0���͵�F��0��![]() ����
����
��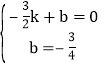 �����
����� ��
��
��ֱ��l�Ľ���ʽΪ![]() ��
��
��B��![]() ��0����D��
��0����D��![]() ����4����
����4����
��![]() �����߶�BD���е�G������Ϊ��
�����߶�BD���е�G������Ϊ��![]() ����2����
����2����
��x=![]() ʱ��
ʱ��![]() ������G��ֱ��l�ϡ�
������G��ֱ��l�ϡ�
�����������ϴ��ڷ��������ĵ�M��
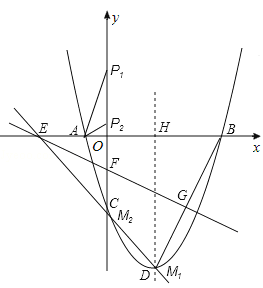
�������ߵĶԳ�����x�ύ��ΪH�����H������Ϊ��![]() ��0����
��0����
��E��![]() ��0����F��0��
��0����F��0��![]() ����B��
����B��![]() ��0����D��
��0����D��![]() ����4����
����4����
��OE=![]() ��OF=
��OF=![]() ��HD=4��HB=
��HD=4��HB=![]() ��
��![]() =2��
=2��
��![]() ����OEF=��HDB��
����OEF=��HDB��
���OEF�ס�HDB�����OFE=��HBD��
�ߡ�OEF+��OFE=90�㣬���OEF+��HBD=90�㡣
���EGB=180�㩁����OEF+��HBD��
=180�㩁90��=90�㣬
��ֱ��l���߶�BD�Ĵ�ֱƽ���ߡ�
����D����ֱ��l�ĶԳƵ���ǵ�B��
����M����ֱ��DE�������ߵĽ��㡣
��ֱ��DE�Ľ���ʽΪy=mx+n��
��D��![]() ����4����E��
����4����E��![]() ��0����
��0����
��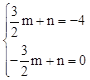 �����
�����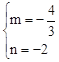 ��
��
��ֱ��DE�Ľ���ʽΪ![]() ��
��
����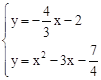 �����
�����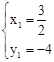 ��
��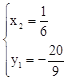 ��
��
�����������ĵ�M���������ǣ�![]() ����4����
����4����![]() ��
��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
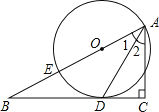
����Ŀ����ͼ����֪��E��ֱ����ABC��б��AB�ϣ���AEΪֱ������O��ֱ�DZ�BC�����ڵ�D��
��1����֤��ADƽ����BAC��
��2����BE=2��BD=4������O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��x1��y1������B��x2��y2����ֱ��y��kx+b��k��0���ϣ���x1y1��x2y2��k����y1y2����9����k��ֵ����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������F��C�ǡ�O�����㣬��![]() ������AC��AF������C��CD��AF��AF�ӳ����ڵ�D������ΪD��
������AC��AF������C��CD��AF��AF�ӳ����ڵ�D������ΪD��
(1)��֤��CD�ǡ�O�����ߣ�
(2)��CD=2![]() �����O�İ뾶��
�����O�İ뾶��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2��2kx+![]() k2��2��0����x1��x2�Ƿ��̵ĸ�����x12��2kx1+2x1x2��5����k��ֵΪ_____��
k2��2��0����x1��x2�Ƿ��̵ĸ�����x12��2kx1+2x1x2��5����k��ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
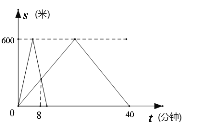
����Ŀ����ĩ�����ˬ���������ģ�С�Դ�үү������·ȥɢ��. �������ڳ���Ϊ600��![]() ��
��![]() ·������������. ���Ǵ�
·������������. ���Ǵ�![]() �س�����С����үү������Ȧһͬ�ص�
�س�����С����үү������Ȧһͬ�ص�![]() �غͿ�ʼ�����ܲ���үү��������ɢ��. ��ͼ��ӳ�����Ǿ���
�غͿ�ʼ�����ܲ���үү��������ɢ��. ��ͼ��ӳ�����Ǿ���![]() �ص�·��
�ص�·��![]() ���ף���С���ܲ���ʱ��
���ף���С���ܲ���ʱ��![]() �����ӣ��IJ��ֹ�ϵͼ�����Ǹ��Ե���
�����ӣ��IJ��ֹ�ϵͼ�����Ǹ��Ե���![]() �ػ�
�ػ�![]() �غ�������ͷ����ͷת��ʱ����Բ��ƣ�. ��С���ܲ����������������Ĵ������������ص���Ϊ_______��.
�غ�������ͷ����ͷת��ʱ����Բ��ƣ�. ��С���ܲ����������������Ĵ������������ص���Ϊ_______��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���ACB=90������ABC=60����BC=2cm��DΪBC���е㣬������E��1cm/s���ٶȴ�A�����������A��B��A�ķ����˶�����E����˶�ʱ��Ϊt�루0��t��6��������DE������BDE��ֱ��������ʱ��t��ֵΪ

A��2 B��2.5��3.5 C��3.5��4.5 D��2��3.5��4.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
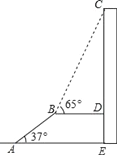
����Ŀ����ͼ��AB�dz�Ϊ10m����б��Ϊ37�����Զ����ݣ�ƽ̨BD���¥CE��ֱ���������AB�ij�����ȣ���B����ô�¥����C������Ϊ65�������¥CE�ĸ߶ȣ��������������.
���ο����ݣ�sin37���![]() ��tan37���
��tan37���![]() ��sin65���
��sin65���![]() ��tan65���
��tan65���![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
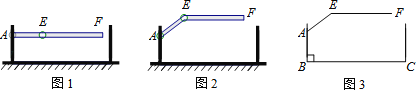
����Ŀ��ij���³�����ڴ���װ�ˡ�����ʽ���ˡ�����ͼ1��ʾ����A������ת����֧�㣬��E���������ε�����㣮����������ʱ������AEF���ֻ��������ͼ2��ʾ��λ�ã���ʾ��ͼ��ͼ3��ʾ�����˿��Ⱥ��Բ��ƣ�������AB��BC��EF��BC����AEF=143����AB=AE=1.2�ף���ô�ʺϸõ��³���ij����߱�־��Ϊ�� �����ο����ݣ�sin37���0.60��cos37���0.80��tan37���0.75��
A�� B��
B�� C��
C�� D��
D��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com