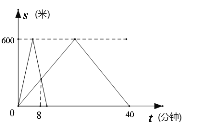
【题目】周末秋高气爽，阳光明媚，小赵带爷爷到滨江路去散步. 祖孙俩在长度为600米的
、
路段上往返行走. 他们从地出发，小赵陪爷爷走了两圈一同回到地后，就开始匀速跑步，爷爷继续匀速散步. 如图反映了他们距离地的路程
（米）与小赵跑步的时间
（分钟）的部分关系图（他们各自到达地或地后立即调头，调头转身时间忽略不计）. 则小赵跑步过程中祖孙俩第四次与第五次相遇地点间距为_______米.
科目：初中数学 来源： 题型：
【题目】抛物线y=x2+bx+c过点（2，-2）和（-1，10），与x轴交于A、B两点，与y轴交于C点．
（1）求抛物线的解析式．
（2）求△ABC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明根据学习函数的经验，对函数y=x+
的图象与性质进行了探究．
下面是小明的探究过程，请补充完整：
（1）函数y=x+的自变量x的取值范围是_____．
（2）下表列出了y与x的几组对应值，请写出m，n的值：m=_____，n=_____；
x | … | ﹣3 | ﹣2 | ﹣1 | ﹣ | ﹣ |
|
| 1 | 2 | 3 | 4 | … |
y | … | ﹣ | ﹣ | ﹣2 | ﹣ | ﹣ | m |
| 2 |
| n |
| … |
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；
（4）结合函数的图象，请完成：
①当y=﹣
时，x=_____．
②写出该函数的一条性质_____．
③若方程x+=t有两个不相等的实数根，则t的取值范围是_____．
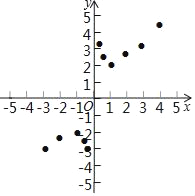
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数
（a≠0）的图象如图所示，
有下列结论：
①a、b同号；
②当x=1和x=3时，函数值相等；
③4a+b=0；
④当-1＜x＜5时，y＜0．
其中正确的有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线
的顶点为点D，并与x轴相交于A、B两点（点A在点B的左侧），与y轴相交于点C．
（1）求点A、B、C、D的坐标；
（2）在y轴的正半轴上是否存在点P，使以点P、O、A为顶点的三角形与△AOC相似？若存在，求出点P的坐标；若不存在，请说明理由；
（3）取点E（
，0）和点F（0，
），直线l经过E、F两点，点G是线段BD的中点．
①点G是否在直线l上，请说明理由；
②在抛物线上是否存在点M，使点M关于直线l的对称点在x轴上？若存在，求出点M的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读材料：若关于x的一元二次方程
的根均为整数，称该方程为“快乐方程”. 我们发现任何一个“快乐方程”的判别式
一定为完全平方数. 规定
为该“快乐方程”的“快乐数”. 若有另一个“快乐方程”
的“快乐数”为
且满足
，则称
互为“乐呵数”. 例如：“快乐方程”
的两根均为整数，其判别式
，其“快乐数”
（1）“快乐方程”
的“快乐数”为 ，若关于x的一元二次方程
（m为整数，且5＜m＜22）是“快乐方程”，求其“快乐数”；
（2）若关于x的一元二次方程
与
（m、n均为整数）都是“快乐方程”，且其“快乐数”互为“乐呵数”，求n的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
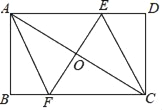
【题目】如图，已知AC是矩形ABCD的对角线，AC的垂直平分线EF分别交BC、AD于点E和F，EF交AC于点O．
（1）求证：四边形AECF是菱形；
（2）若AC＝8，EF＝6，求菱形的边长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在ABCD中，AB=6，AD=9，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE，垂足为G，BG=
，则△CEF的周长为（ ）
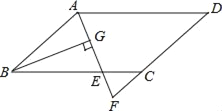
A. 8 B. 9.5 C. 10 D. 11.5
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，BC是路边坡角为30°，长为10米的一道斜坡，在坡顶灯杆CD的顶端D处有一探射灯，射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°（图中的点A、B、C、D、M、N均在同一平面内，CM∥AN）．
（1）求灯杆CD的高度；
（2）求AB的长度（结果精确到0.1米）．（参考数据：
=1.73．sin37°≈060，cos37°≈0.80，tan37°≈0.75）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
