练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
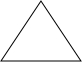
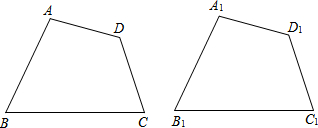
    20．星期天早晨茗茗陪爷爷出门散步，他们所走的路线组成一个等边三角形，如图所示，下列可以正确表示他们离家的距离s与时间t的函数图象的是（　　）
    A．B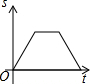．C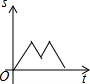．D．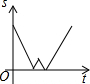

    分析 分析图象可知：该图象是路程与时间的关系，先离家逐渐变远，到达三角形的第一个顶点，离家最远；然后走到第二条边的中点时距离越来越小，后又越来越大，到达第二个顶点有达到最大；走到第三条边上时，离家距离在逐渐变近，最后变为0；由此选择图象得出答案即可．

    解答 解：由题意可知：先离家逐渐变远，到达三角形的第二个顶点，离家最远；然后走到第二条边的中点时距离越来越小，后又越来越大，到达第三个顶点有达到最大；走到第三条边上时，离家距离在逐渐变近，最后变为0；符合题意的图象是C．
    故选：C．

    点评 此题考查了动点函数的图象，要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件，结合实际意义得到正确的结论．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    11．篮球场上，小东、小西、小南、小北四位同学打算用手心手背的方法来组成两个二人小组打比赛，组队规则如下：他们四人将右手同时从背后伸出，并随机让自己的手背或手心朝上，若恰好只有两人手心朝上，则手心朝上的这两人为一队，余下的两人为一队；若没有出现这样的结果则重复上述过程．试用列表或树状图的方法解决下列问题：
    （1）共有多少种等可能结果？
    （2）他们只伸出手一次就恰好分为两个二人小队的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．从正方形纸片上截去3cm宽的一个矩形，余下的面积是40cm2，则原正方形纸片的面积是（　　）
    A．68cm2B．86cm2C．64cm2D．56cm2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图1，平面直角坐标系中，抛物线y=ax2+bx+c与x轴交于A、B两点，与y轴交于点C，顶点为M．D在y轴上，OB=OD=3，OA=5．
    （1）试用含a的式子表示点M的坐标；
    （2）若S△ABC-S△ACM=$\frac{50}{3}$；
    ①求抛物线y=ax2+bx+c的解析式；
    ②如图2，将△BOD绕点O沿逆时针方向旋转α（0°＜α≤180°）得到△B′OD′，直线AD与BC相交于点Q，求点Q纵坐标的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．我们借助学习“三角形全等的判定”获得的经验与方法，对“全等四边形的判定”进行探究．
    规定：
    （1）四条边对应相等，四个角对应相等的两个四边形全等．
    （2）在两个四边形中，我们把“一条边对应相等”或“一个角对应相等”称为一个条件．
    【初步思考】
    满足4个条件的两个四边形不一定全等，如边长相等的正方形与菱形就不一定全等．类似地，我们容易知道两个四边形全等至少需要5个条件．
    【深入探究】
    小莉所在学习小组进行了研究，她们认为5个条件可分为以下四种类型：
    Ⅰ一条边和四个角对应相等；
    Ⅱ二条边和三个角对应相等；
    Ⅲ三条边和二个角对应相等；
    Ⅳ四条边和一个角对应相等．
    （1）小明认为“Ⅰ一条边和四个角对应相等”的两个四边形不一定全等，请你举例说明．
    （2）小红认为“Ⅳ四条边和一个角对应相等”的两个四边形全等，请你结合下图进行证明．
    已知：如图，四边形ABCD和四边形A1B1C1D1中，AB=A1B1，BC=B1C1，CD=C1D1，DA=D1A1，∠B=∠B1．
    求证：四边形ABCD≌四边形A1B1C1D1．
    证明：

    （3）小刚认为还可以对“Ⅱ二条边和三个角对应相等”进一步分类，他以四边形ABCD和四边形A1B1C1D1为例，分为以下几类：
    ①AB=A1B1，AD=A1D1，∠A=∠A1，∠B=∠B1，∠C=∠C1；
    ②AB=A1B1，AD=A1D1，∠A=∠A1，∠B=∠B1，∠D=∠D1；
    ③AB=A1B1，AD=A1D1，∠B=∠B1，∠C=∠C1，∠D=∠D1；
    ④AB=A1B1，CD=C1D1，∠A=∠A1，∠B=∠B1，∠C=∠C1．
    其中能判定四边形ABCD和四边形A1B1C1D1全等的是①②③（填序号），概括可得一个“全等四边形的判定方法”，这个判定方法是有一组邻边和三个角对应相等的两个四边形全等．
    （4）小亮经过思考认为也可以对“Ⅲ三条边和二个角对应相等”进一步分类，请你仿照小刚的方法先进行分类，再概括得出一个不同于（3）中所示的全等四边形的判定方法．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图1，在平面直角坐标系中，点A、B、C的坐标分别为（-8，0），（-5，0），（0，-8），点P，E分别从点A，B同时出发沿x轴正方向运动，同时点D从点C出发沿y轴正方向运动．以PD，PE为邻边构造平行四边形EPDF，已知点P，D的一点速度均为每秒2个单位，点E的运动速度为每秒1个单位，运动时间为t秒．
    （1）当0＜t＜3时，PE=3-t（用含t的代数式表示）；
    （2）记平行四边形的面积为S，当S=12时，求t的值；
    （3）如图2，当0＜t＜4时，过点P的作抛物线y=ax2+bx+c交x轴于另一点为H（点H在点P的右侧），若PH=6，且该二次函数的最大值不变均为$\frac{9}{4}$．
    ①当t=2时，试判断点F是否恰好落在抛物线y=ax2+bx+c上？并说明理由；
    ②若点D关于直线EF的对称点Q恰好落在抛物线y=ax2+bx+c，请直接写出t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

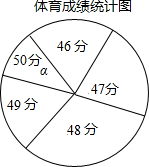    12．郑州市某中学九年级学生体育中招考试后，为了解本校学生体育测试成绩情况，现从中随机抽取部分学生的体育成绩统计如下，其中如扇形统计图中的圆心角α为36°
    九年级学生体育中招成绩统计表
    体育成绩（分）人数（人）百分比（%）
    46816
    4724
    4815
    49m
    50
    根据上面提供的信息，回答下列问题：
    （1）被抽测学生的体育成绩的样本容量为50，m=10；抽取的部分学生体育成绩的中位数为48分；
    （2）请计算被抽测学生的中考体育的平均成绩；
    （3）已知该校九年级共有500名学生，如果体育成绩达48分以上（含48分）为优秀，请估计该校九年级学生体育成绩达到优秀的总人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．计算-2a2b3÷ab2=-2ab．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．（1）（2a+1）2-（2a+1）（-1+2a）
    （2）$\frac{1}{2}$a2bc3•（-2a2b2c）2
    （3）（2x-y）（4x2-y2）（2x+y）
    （4）（54x2y-108xy2-36xy）÷18xy
    （5）（2x+3y）（2x-3y）-（2x+3y）2．

    查看答案和解析>>

    同步练习册答案