
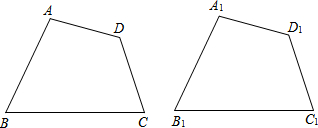
分析 (1)可以利用正方形与矩形进行说明;
(2)根据四条边对应相等,和一个角对应相等,结合图形即可写出已知与求证.证明时可以连接AC、A1 C1,转化为证明△ABC≌△A1B1C1,和△ACD≌△A1C1D1.即可证得;
(3)根据条件能证明①②③中△ABD≌△A1B1D1(SAS),和△BCD≌△B1C1D1(AAS或ASA),从而利用全等三角形的性质与等式的性质得出两个四边形四条边对应相等,四个角对应相等,因而这两个四边形全等;
(4)写出三条边对应相等,和二个角对应相等分情况进行讨论的情况即可.
解答 解:(1)如正方形与矩形有一条边对应相等,但显然不一定全等.
(2)已知:如图,四边形ABCD和四边形A1 B1 C1 D1中,AB=A1B1,BC=B1C1,CD=C1D1,DA=D1A1,∠B=∠B1.
求证:四边形ABCD≌四边形A1B1C1D1.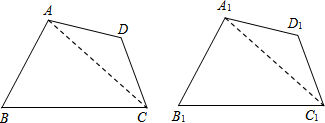
证明:连接AC、A1C1.
∵AB=A1B1,∠B=∠B1,BC=B1C1,
∴△ABC≌△A1B1C1,
∴AC=A1C1,∠BAC=∠B1A1C1,∠BCA=∠B1C1A1.
又∵CD=C1D1,DA=D1A1,
∴△ACD≌△A1C1D1.
∴∠D=∠D1,∠DAC=∠D1A1C1,∠DCA=∠D1C1A1,
∴∠BAD=∠B1A1D1,∠BCD=∠B1C1D1,
∴四边形ABCD≌四边形A1B1C1D1;
(3)①②③;
有一组邻边和三个角对应相等的两个四边形全等.
(4)分为四类:
①AB=A1B1,BC=B1C1,CD=C1D1,∠A=∠A1,∠B=∠B1;
②AB=A1B1,BC=B1C1,CD=C1D1,∠A=∠A1,∠C=∠C1;
③AB=A1B1,BC=B1C1,CD=C1D1,∠A=∠A1,∠D=∠D1;
④AB=A1B1,BC=B1C1,CD=C1D1,∠B=∠B1,∠C=∠C1.
有三条边和这三条边中每一组邻边的夹角对应相等的两个四边形全等.
故答案为(2)四边形ABCD和四边形A1 B1 C1 D1中,AB=A1B1,BC=B1C1,CD=C1D1,DA=D1A1,∠B=∠B1;四边形ABCD≌四边形A1B1C1D1;
(3)①②③;有一组邻边和三个角对应相等的两个四边形全等.
点评 本题考查了四边形综合题,涉及的知识点有:四边形的全等,三角形全等的判定与性质,解题的关键是注意:多边形的全等可以通过作辅助线转化为证明三角形全等的问题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 星期天早晨茗茗陪爷爷出门散步,他们所走的路线组成一个等边三角形,如图所示,下列可以正确表示他们离家的距离s与时间t的函数图象的是( )
星期天早晨茗茗陪爷爷出门散步,他们所走的路线组成一个等边三角形,如图所示,下列可以正确表示他们离家的距离s与时间t的函数图象的是( )| A. |  | B. | 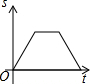 | C. | 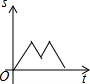 | D. | 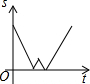 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
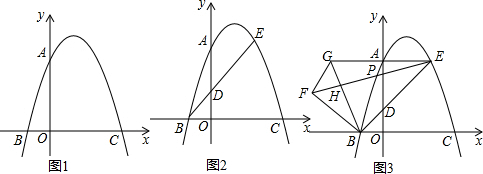
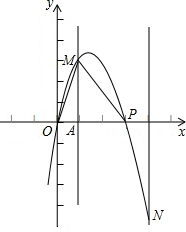 如图,在平面直角坐标系中,点P从原点O出发,沿x轴向右以每秒一个单位长度的速度运动t秒(t>0),抛物线y=-x2+bx+c经过点O和点P.
如图,在平面直角坐标系中,点P从原点O出发,沿x轴向右以每秒一个单位长度的速度运动t秒(t>0),抛物线y=-x2+bx+c经过点O和点P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com