
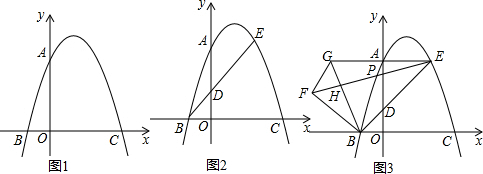
���� ��1����y=0�������������x��Ľ������꣬�����߶�BC�ij��ȣ�����AO=$\frac{3}{4}$BC���ɵõ�A�����ꣻ
��2����EI��x����I���á�BOD�ס�BIE���ɵ�$\frac{BO}{BI}$=$\frac{DO}{EI}$�����������E�����ꣻ
��3���ӳ�GF��x����M����GN��x����N����BF���ڵ�K������EK���ӳ�BF��ֱ��EA��L����BW��EA��W��֤����GBMΪ���������Σ��Ӷ�֤�á�BWEΪ����ֱ�������Σ��ҡ�BELΪֱ�������Σ��á�NBKΪ���������Σ����ݹ��ɶ����������G�����꣬���BG��EF�����꣬����ֱ��EF���������ཻ�ڵ�P�����������P�������������߶εĹ�ʽ����������߶�EP�ij���
���  �⣺��1����y=0ʱ��kx2-2kx-3k=0�����x1=-1��x2=3����B��-1��0����C��3��0����
�⣺��1����y=0ʱ��kx2-2kx-3k=0�����x1=-1��x2=3����B��-1��0����C��3��0����
��BC=3-1��-1��=4��
��AO=$\frac{3}{4}$BC=3����A��0��3����
��A��0��3������y=kx2-2kx-3k��-3k=3�����k=-1��
�������߽���ʽΪy=-x2+2x+3��
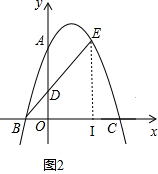
��2����EI��x����I����ͼ2��
��E��t��-t2+2t+3����t��0������OI=t��OD=$\frac{1}{2}$t��
��OD��EI��
���BOD�ס�BIE��
��$\frac{BO}{BI}$=$\frac{DO}{EI}$����$\frac{1}{t+1}$=$\frac{\frac{1}{2}t}{-{t}^{2}+2t+3}$��
������t2-t-2=0�����t1=-1����ȥ����t2=2��
��E��������2��3����
��3����ͼ3���ӳ�GF��x����M����GN��x����N����BF���ڵ�K������EK���ӳ�BF��ֱ��EA��L����BW��EA��W��
��A��0��3����E��2��3����
��AE��x�ᣬ
��GE��GN��
���2=90��-��3��
��BH��EF��
���GHE=90�㣬
���2=90��-��1��
���1=��3��
�ߡ�2=90��-$\frac{1}{2}$��BGF��
���3=$\frac{1}{2}$��BGM��
���3=��4��
����GN��BM��
���GBM����������
��BN=MN��
��BW=EW=3��
���BWEΪ����ֱ�������Σ�
���BELΪֱ�������Σ�
��DBO=45�㣬
��BF��BE��
���NBK=45�㣬
���NBK����������
��BN=m����KN=m��BK=$\sqrt{2}$m��
��Rt��GKE��KE2=GK2+GE2=��3-m��2+42��
��Rt��BKE��KE2=BK2+BE2=��$\sqrt{2}$m��2+��3$\sqrt{2}$��2��
��ã�x1=1��x2=-7���������⣬��ȥ����
���G��-2��3����
��ֱ��BG�Ľ���ʽΪ��y=kx+b����B��-1��0����G��-2��3����ֱ��BG�ϣ�
��$\left\{\begin{array}{l}{-k+b=0}\\{-2k+b=3}\end{array}\right.$����ã�$\left\{\begin{array}{l}{k=-3}\\{b=-3}\end{array}\right.$��
��ֱ��BG��y=-3x-3��
��ֱ��EF��BG��
����ֱ��FE�Ľ���ʽΪ��y=$\frac{1}{3}$x+b1����E��2��3����ֱ��FE�ϣ�
��$\frac{1}{3}��2+{b}_{1}=3$����ã�b1=$\frac{7}{3}$��
��ֱ��EF��y=$\frac{1}{3}x+\frac{7}{3}$��
���������飬��$\left\{\begin{array}{l}{y=-{x}^{2}+2x+3}\\{y=\frac{1}{3}x+\frac{7}{3}}\end{array}\right.$����ã�$\left\{\begin{array}{l}{{x}_{1}=-\frac{1}{3}}\\{{y}_{1}=\frac{20}{9}}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{2}=2}\\{{y}_{2}=3}\end{array}\right.$����ȥ����
���P��$-\frac{1}{3}$��$\frac{20}{9}$����
��PE=$\sqrt{��-\frac{1}{3}-2��^{2}+��\frac{20}{9}-3��^{2}}=\frac{7\sqrt{10}}{9}$��
���� ������Ҫ������κ������ۺ�Ӧ�ã�����С�⣬�������⻭��ͼ�Σ����Ӻ��ʵĸ������ǽ������Ļ������ܹ�������õ��������Ρ�ֱ�������Σ�����ϵ�������������깫ʽ��֪ʶ�ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a2+a2=a4 | B�� | 2��a-b��=2a-b | C�� | a3•a2=a5 | D�� | ��-b2��3=-b5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
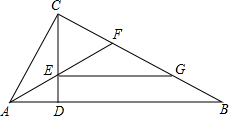 ��ͼ����Rt��ABC�У���ACB=90�㣬CD��AB��D�㣬AFƽ�֡�BAC��CD��E�㣬��BC��F�㣬EG��AB��BC��G�㣮
��ͼ����Rt��ABC�У���ACB=90�㣬CD��AB��D�㣬AFƽ�֡�BAC��CD��E�㣬��BC��F�㣬EG��AB��BC��G�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
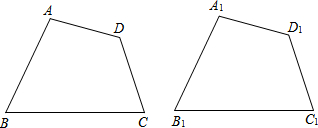
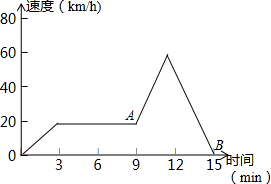 ����ͼ�ش��������⣺
����ͼ�ش��������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
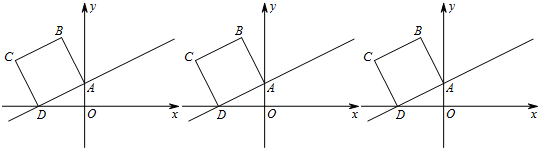
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com