
���� ��1�����ʽ�յ�ÿ̨�IJɹ�����xԪ�������ÿ̨�IJɹ�����yԪ�����ݲɹ��۸�=���ۡ����������г�����x��y�Ķ�Ԫһ�η����飬�ⷽ���鼴�ɵó����ۣ�
��2�����ٹ����յ�ą�������ȣ�70-a��̨�����ݲɹ��۸�=���ۡ����������г�����a��һԪһ�β���ʽ���ⲻ��ʽ���ɵó����ۣ�
��� �⣺��1�����ʽ�յ�ÿ̨�IJɹ�����xԪ�������ÿ̨�IJɹ�����yԪ��
�������⣬��$\left\{\begin{array}{l}{8x+20y=17400}\\{10x+30y=22500}\end{array}\right.$��
��$\left\{\begin{array}{l}{x=1800}\\{y=150}\end{array}\right.$��
�𣺹�ʽ�յ�ÿ̨�IJɹ�����1800Ԫ�������ÿ̨�IJɹ�����150Ԫ��
��2�����ٹ����յ�ą�������ȣ�70-a��̨��
����֪����1800a+150��70-a����30000��
��ã�a��11$\frac{9}{11}$��
�ʸþ�Ӫҵ�������ٹ����յ�11̨��
���� ���⿼���˶�Ԫһ�η������Ӧ���Լ���һԪһ�β���ʽ������Ĺؼ��ǣ���1���г�����x��y�Ķ�Ԫһ�η����飻��2���г�����a��һԪһ�β���ʽ���������ڻ����⣬�ѶȲ������������Ŀʱ������������ϵ�г����̣��������ʽ���ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
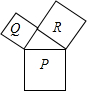 ��ͼ���ֱ���ֱ�������εı߳�Ϊ��������������P��Q��R����������P��Q������ֱ���4��1����������R�ı߳���$\sqrt{3}$��
��ͼ���ֱ���ֱ�������εı߳�Ϊ��������������P��Q��R����������P��Q������ֱ���4��1����������R�ı߳���$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
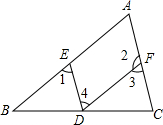 ��ͼ�������и����������£������ж�AB��DF���ǣ�������
��ͼ�������и����������£������ж�AB��DF���ǣ�������| A�� | ��A+��2=180�� | B�� | ��A=��3 | C�� | ��1=��4 | D�� | ��1=��A |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com