
分析 根据所给线段长分成几种情况,然后再根据三角形三边关系:三角形两边之和大于第三边,三角形的两边差小于第三边可得答案.
解答 解:以其中的三条线段为边组成三角形的有:①2cm,3cm,6cm;②2cm,3cm,7cm;③2cm,3cm,8cm;④2cm,6cm,7cm;⑤2cm,6cm,8cm;⑥2cm,7cm,8cm;⑦3cm,6cm,7cm,⑧3cm,6cm,8cm,⑨3cm,7cm,8cm;6cm,7cm,8cm共有10种情况,
可以构成三角形的有6个,
故答案为:6.
点评 此题主要考查了三角形的三边关系,关键是掌握三角形三边关系,写出所有情况后,然后再利用三角形的三边关系判断.


科目:初中数学 来源: 题型:解答题
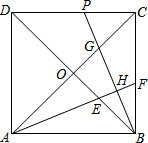 已知正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于点E、F,作BH⊥AF,垂足为H,BH的延长线分别交AC、CD于点G、P.
已知正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于点E、F,作BH⊥AF,垂足为H,BH的延长线分别交AC、CD于点G、P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
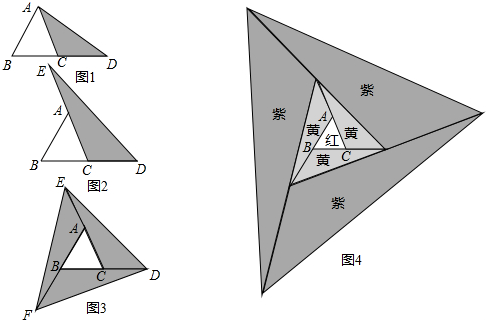
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
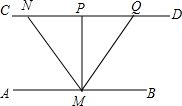 请你将下面的证明补充完整,并在括号内填写推理依据.
请你将下面的证明补充完整,并在括号内填写推理依据.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com