
【题目】如图,已知∠AOB=160°,OD是∠AOB内任意一条射线,OE平分∠AOD,OC平分∠BOD.
(1)求∠EOC的度数;
(2)若∠BOC=19°,求∠EOD的度数.

【答案】(1)80°;(2)61°.
【解析】
(1)先根据角平分线定义得到∠EOD=![]() ∠AOD,∠DOC=
∠AOD,∠DOC=![]() ∠DOB,再求出∠EOC=∠EOD+∠DOC=
∠DOB,再求出∠EOC=∠EOD+∠DOC=![]() ∠AOB=80°;
∠AOB=80°;
(2)先根据角平分线定义得到∠DOB=2∠BOC=38°,再求出∠AOD=∠AOB﹣∠DOB=122°,然后根据角平分线定义得出∠EOD=![]() ∠AOD=61°.
∠AOD=61°.
解:(1)∵OE平分∠AOD,OC平分∠BOD,
∴∠EOD=![]() ∠AOD,∠DOC=
∠AOD,∠DOC=![]() ∠DOB,
∠DOB,
∴∠EOC=∠EOD+∠DOC=![]() ∠AOD+
∠AOD+![]() ∠DOB=
∠DOB=![]() (∠AOD+∠DOB)=
(∠AOD+∠DOB)=![]() ∠AOB=80°;
∠AOB=80°;
(2)∵OC平分∠BOD,
∴∠DOB=2∠BOC=38°,
∴∠AOD=∠AOB﹣∠DOB=122°,
∵OE平分∠AOD,
∴∠EOD=![]() ∠AOD=61°.
∠AOD=61°.


科目:初中数学 来源: 题型:
【题目】用100厘米长的铅丝,弯折成一个长方形的模型.
(1)设长方形的面积为S平方厘米,长方形的长为![]() 厘米,用
厘米,用![]() 的式子表示S;
的式子表示S;
(2)当S=400平方厘米时,求![]() 的值;
的值;
(3)当S=625平方厘米时,求![]() 的值;
的值;
(4)S的值会不会为700平方厘米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,M、N分别是线段AC、BC的中点,
![]()
(1)若AC=7cm,BC=5cm,求线段MN的长;
(2)若AB=a,点C为线段AB上任意一点,你能用含a的代数式表示MN的长度吗?若能,请写出结果与过程,若不能,请说明理由;
(3)若将(2)中“点C为线段AB上任意一点”改为“点C为直线AB上任意一点”,其余条件不变,(2)中的结论是否仍然成立?请画图并写出说明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍.小颖在小亮出发后50min才乘上缆车,缆车的平均速度为180m/min.设小亮出发xmin后行走的路程为ym,图中的折线表示小亮在整个行走过程中y与x的函数关系.
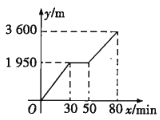
(1)小亮行走的总路程是________m;他途中休息了________min.
(2)①当![]() 时,求y与x的函数关系式.
时,求y与x的函数关系式.
②当小颖到达缆车终点时,小亮离缆车终点的路程是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,AC平分DAB,12,试说明AB与CD的位置关系,并予以证明:
(2)如图2,在(1)的结论下,AB的下方点P满足ABP30,G是CD上任一点,PQ平分BPG,PQ∥GN,GM平分DGP,下列结论:
①DGPMGN的值不变;
②MGN的度数不变.
可以证明,只有一个是正确的,请你做出正确的选择并求值.
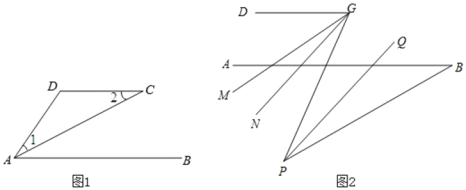
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校餐厅计划购买12张餐桌和一批餐椅,现从甲、乙两商场了解到:同一型号的餐桌报价每张均为200元,餐椅报价每把均为50元.甲商场称:每购买一张餐桌赠送一把餐椅;乙商场规定:所有餐桌椅均按报价的八五折销售.那么多少餐椅,到甲商场购买更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
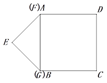
【题目】如图,边长为4个单位长度的正方形ABCD的边AB与等腰直角三角形EFG的斜边FG重合,△EFG
以每秒1个单位长度的速度沿BC向右匀速运动(保持FG⊥BC),当点E运动到CD边上时△EFG停止
运动.设△EFG的运动时间为t秒,△EFG与正方形ABCD重叠部分的面积为S,则S关于t的函数大
致图象为( )
A. 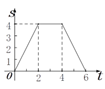 B.
B. 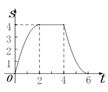 C.
C. 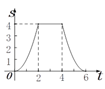 D.
D. 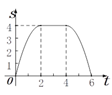
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,D、F是AB边上的两点,以DF为直径的⊙O与BC相交于点E,连接EF,过F作FG⊥BC于点G,其中∠OFE=![]() ∠A.
∠A.
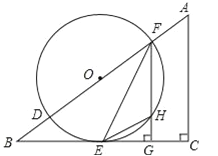
(1)求证:BC是⊙O的切线;
(2)若sinB=![]() ,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点D 作![]() 于点E,点F在边CD上,DF=BE,连接AF,BF.
于点E,点F在边CD上,DF=BE,连接AF,BF.

(1)求证:四边形EBFD是矩形;
(2)若AE=3,DE=4,DF=5,求证:AF平分![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com