
【题目】某校餐厅计划购买12张餐桌和一批餐椅,现从甲、乙两商场了解到:同一型号的餐桌报价每张均为200元,餐椅报价每把均为50元.甲商场称:每购买一张餐桌赠送一把餐椅;乙商场规定:所有餐桌椅均按报价的八五折销售.那么多少餐椅,到甲商场购买更优惠?
【答案】当购买的餐椅大于等于9少于32把时,到甲商场购买更优惠.
【解析】
本题中去甲商场购买所花的费用=餐桌的单价×购买的餐桌的数量+餐椅的单价×实际购买的餐椅的数量(注意要减去赠送的椅子的数量).去乙商场购买所花的费用=(购买的餐桌花的钱+购买餐椅花的钱)×8.5折.如果设餐椅的数量为x,那么可用x表示出到甲、乙两商场购买所需要费用.然后根据“甲商场购买更优惠”,让甲的费用小于乙的费用,得出不等式求出x的取值范围,然后得出符合条件的值.
设学校计划购买x把餐椅,到甲、乙两商场购买所需要费用分别为y![]() 、y
、y![]() ,
,
①当椅子的数量小于12时,
y![]() =2400;
=2400;
y![]() =(200×12+50x)×85%;
=(200×12+50x)×85%;
当y![]() <y
<y![]() 时,2400<2040+
时,2400<2040+![]() x,
x,
解得:x>8.47,即x9.
②当椅子的数量大于等于12时,
y![]() =200×12+50(x12),
=200×12+50(x12),
即:y![]() =1800+50x;
=1800+50x;
y![]() =(200×12+50x)×85%,
=(200×12+50x)×85%,
即y![]() =2040+
=2040+![]() x;
x;
当y![]() <y
<y![]() 时,1800+50x<2040+
时,1800+50x<2040+![]() x,
x,
∴x<32,又根据题意可得:x12,
∴12x<32,
综上所述,当购买的餐椅大于等于9少于32把时,到甲商场购买更优惠.


科目:初中数学 来源: 题型:
【题目】公园内要铺设一段长方形步道,须用一些型号相同的灰色正方形地砖和一些型号相同 的白色等腰直角三角形地砖按如图所示方式排列.

(1) 若排列正方形地砖40块,则需使用三角形地砖____________块;
(2) 若排列三角形地砖2 020块,则需使用正方形地砖____________块.
查看答案和解析>>
科目:初中数学 来源: 题型:
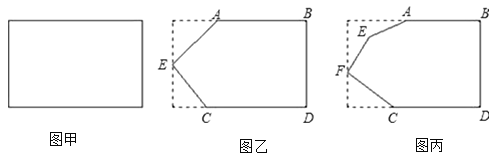
【题目】如图甲表示一个长方形纸片.
①如图乙,将图甲的一侧剪两刀后剪出3个角,那么AEC(________________);
②如图丙,将图甲的一侧剪三刀后剪出4个角,那么AEFC(________);
③按照上述剪法,将图甲的一侧剪出n个角,那么这n个角的和=(________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D。
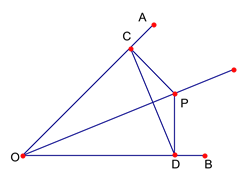
(1)求证:∠PCD=∠PDC;(2)求证:OP垂直平分线段CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=160°,OD是∠AOB内任意一条射线,OE平分∠AOD,OC平分∠BOD.
(1)求∠EOC的度数;
(2)若∠BOC=19°,求∠EOD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
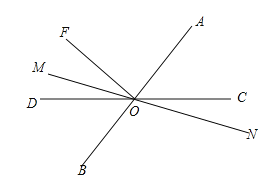
【题目】如图,直线AB、CD、MN相交与点O,FO⊥BO,OM平分∠DOF
(1)请直接写出图中所有与∠AON互余的角: .
(2)若∠AOC=![]() ∠FOM,求∠MOD与∠AON的度数.
∠FOM,求∠MOD与∠AON的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织七年级学生参加冬令营活动,本次冬令营活动分为甲、乙、丙三组进行.如图,条形统计图和扇形统计图反映了学生参加冬令营活动的报名情况,请你根据图中的信息回答下列问题:
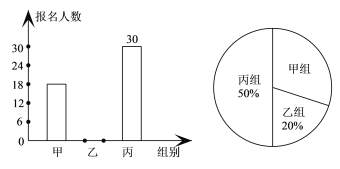
(1)七年级报名参加本次活动的总人数为 ,扇形统计图中,表示甲组部分的扇形的圆心角是 度;
(2)补全条形统计图;
(3)根据实际需要,将从甲组抽调部分学生到丙组,使丙组人数是甲组人数的3倍,则应从甲组抽调多少名学生到丙组?
查看答案和解析>>
科目:初中数学 来源: 题型:
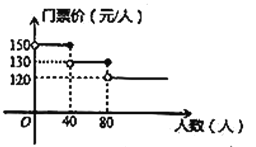
【题目】我市某风景区门票价格如图所示,有甲、乙两个旅行团队,计划在端午节期间到该景点游玩,两团队游客人数之和为100人,乙团队人数不超过40人.设甲团队人数为![]() 人,如果甲、乙两团队分别购买门票,两团队门票款之和为
人,如果甲、乙两团队分别购买门票,两团队门票款之和为![]() 元.
元.
(1)直接写出![]() 关于
关于![]() 的函数关系式,并写出自变
的函数关系式,并写出自变![]() 的取值范围;
的取值范围;
(2)若甲团队人数不超过80人,计算甲、乙两团队联合购票比分别购票最多可节约多少钱?
(3)端午节之后,该风景区对门票价格作了如下调整:人数不超过40人时,门票价格不变,人数超过40人但不超过80人时,每张门票降价![]() 元;人数超过80人时,每张门票降价
元;人数超过80人时,每张门票降价![]() 元.在(2)的条件下,若甲、乙两个旅行团端午节之后去游玩联合购票比分别购票最多可节约3900元,求
元.在(2)的条件下,若甲、乙两个旅行团端午节之后去游玩联合购票比分别购票最多可节约3900元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校需要添置教师办公桌椅A、B两型共200套,已知2套A型桌椅和1套B型桌椅共需2000元,1套A型桌椅和3套B型桌椅共需3000元.
(1)求A,B两型桌椅的单价;
(2)若需要A型桌椅不少于120套,B型桌椅不少于70套,平均每套桌椅需要运费10元.设购买A型桌椅x套时,总费用为y元,求y与x的函数关系式,并直接写出x的取值范围;
(3)求出总费用最少的购置方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com