
【题目】如图,在平行四边形ABCD中,过点D 作![]() 于点E,点F在边CD上,DF=BE,连接AF,BF.
于点E,点F在边CD上,DF=BE,连接AF,BF.

(1)求证:四边形EBFD是矩形;
(2)若AE=3,DE=4,DF=5,求证:AF平分![]()
【答案】见解析
【解析】
(1)根据平行四边形的性质,可得AB与CD的关系,根据平行四边形的判定,可得BFDE是平行四边形,再根据矩形的判定,可得答案;
(2)根据平行线的性质,可得∠DFA=∠FAB,根据等腰三角形的判定与性质,可得∠DAF=∠DFA,根据角平分线的判定,可得答案.
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD.
∵BE∥DF,BE=DF,
∴四边形BFDE是平行四边形。
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是矩形;
(2)∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠DFA=∠FAB.
在Rt△BCF中,由勾股定理,得
BC=![]() =5,
=5,
∴AD=BC=DF=5,
∴∠DAF=∠DFA,
∴∠DAF=∠FAB,
即AF平分∠DAB.


科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=160°,OD是∠AOB内任意一条射线,OE平分∠AOD,OC平分∠BOD.
(1)求∠EOC的度数;
(2)若∠BOC=19°,求∠EOD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
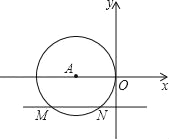
【题目】如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、N两点,若点M的坐标是(﹣8,﹣4),则点N的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
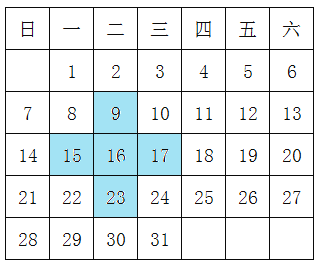
【题目】观察某月的月历,回答下列问题.
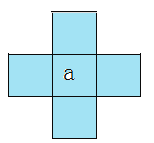
(1)设十字框中间的数为![]() ,求带阴影的十字框中间的5个数的和是多少?
,求带阴影的十字框中间的5个数的和是多少?
(2)小李一家外出游玩了5天,这5天的日期之和是75,小李一家是几号外出的?
(3)在该月的日历上用十字框框出5个数,能使这5个数的和为100吗?如果不能,请说明理由;如果能,请求出十字框中间的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校需要添置教师办公桌椅A、B两型共200套,已知2套A型桌椅和1套B型桌椅共需2000元,1套A型桌椅和3套B型桌椅共需3000元.
(1)求A,B两型桌椅的单价;
(2)若需要A型桌椅不少于120套,B型桌椅不少于70套,平均每套桌椅需要运费10元.设购买A型桌椅x套时,总费用为y元,求y与x的函数关系式,并直接写出x的取值范围;
(3)求出总费用最少的购置方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点C是线段AB的中点,点D是线段BC上一点,下列条件不能确定点D是线段BC的中点的是( )
A.CD=DBB.BD=![]() ADC.2AD=3BCD.3AD=4BC
ADC.2AD=3BCD.3AD=4BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P1是线段AB上一点,AP1=2BP1;点P2是线段P1B上一点,P1P2=2BP2:点P3是线段P2B上一点,P2P3=2BP3 , …请借助所给的图形,计算 ![]() 的结果为________(n为正整数,用含n的代数式表示)
的结果为________(n为正整数,用含n的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校对该校七年级(1)班全体学生的血型做了一次全面调查,根据调查结果绘制了下列两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
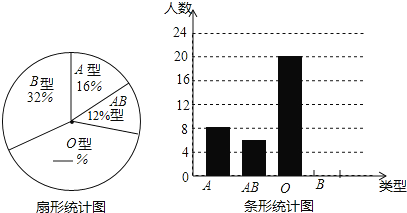
(1)该校七年级(1)班有多少名学生.
(2)求出扇形统计图中“O型”血所对扇形的圆心角的度数.
(3)将条形统计图中“B型”血部分的条形图补充完整.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com