Question

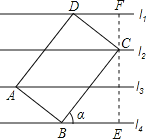
【题目】已知直线l1∥l2∥l3∥l4，相邻两条平行线间的距离均为h，矩形ABCD的四个顶点分别在这四条直线上，放置方式如图所示，AB＝4，BC＝6，则tanα的值等于(　　)

A. B. C. D.

Answer 1

【答案】C

【解析】

过点C作CE⊥l4于点E，延长EC交l1于点F，根据同角的余角相等求出∠α=∠DCF，利用两角对应相等的两三角形相似证明△BEC∽△CFD，再由相似三角形对应边成比例可得BE=h，然后在Rt△BCE中利用锐角的正切值等于对边比邻边列式计算即可得解．

如图，过点C作CE⊥l4于点E，延长EC交l1于点F，

在矩形ABCD中，∠BCD=90°，

∵∠α+∠BCE=90°，∠BCE+∠DCF=180°-90°=90°，

∴∠α=∠DCF，

又∵∠BEC=∠CFD=90°，

∴△BEC∽△CFD，

∴，

即，

∴BE=h，

在Rt△BCE中，∵∠BEC=90°，

∴tanα==，

故选：C．