
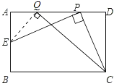
【题目】如图,已知在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 边上的任意一点(不含端点
边上的任意一点(不含端点![]() 、
、![]() ),连接
),连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() .
.

![]() 在线段
在线段![]() 上是否存在不同于
上是否存在不同于![]() 的点
的点![]() ,使得
,使得![]() ?若存在,求线段
?若存在,求线段![]() 与
与![]() 之间的数量关系;若不存在,请说明理由;
之间的数量关系;若不存在,请说明理由;
![]() 当点
当点![]() 在
在![]() 上运动时,对应的点
上运动时,对应的点![]() 也随之在
也随之在![]() 上运动,求
上运动,求![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 是
是![]() 的中点时,满足条件的
的中点时,满足条件的![]() 点不存在.当
点不存在.当![]() 不是
不是![]() 的中点时,总存在这样的点
的中点时,总存在这样的点![]() 满足条件,此时
满足条件,此时![]() ;(2)
;(2)![]() 的取值范围是
的取值范围是![]() .
.
【解析】
(1)假设存在符合条件的Q点,由于PE⊥PC,且四边形ABCD是矩形,易证得△APE∽△DCP,可得APPD=AECD,同理可通过△AQE∽△DCQ得到AQQD=AEDC,则APPD=AQQD,分别用PD、QD表示出AP、AQ,将所得等式进行适当变形即可求得AP、AQ的数量关系.(2)由于BE的最大值为AB的长即2,因此只需求得BE的最小值即可;设AP=x,AE=y,在(1)题中已经证得APPD=AECD,用x、y表示出其中的线段,即可得到关于x、y的函数关系式,根据函数的性质即可求得y的最大值,由此可求得BE的最小值,即可得到BE的取值范围.
![]() 假设存在这样的点
假设存在这样的点![]() ;
;
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
同理可得![]() ;
;
∴![]() ,即
,即![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ;
;
∵![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ,即
,即![]() 不能是
不能是![]() 的中点,
的中点,
∴当![]() 是
是![]() 的中点时,满足条件的
的中点时,满足条件的![]() 点不存在.
点不存在.
当![]() 不是
不是![]() 的中点时,总存在这样的点
的中点时,总存在这样的点![]() 满足条件,此时
满足条件,此时![]() .
.
![]() 设
设![]() ,
,![]() ,由
,由![]() 可得
可得![]() ,
,
∴![]() ,
,
∴当![]() (在
(在![]() 范围内)时,
范围内)时,![]() ;
;
而此时![]() 最小为
最小为![]() ,
,
又∵![]() 在
在![]() 上运动,且
上运动,且![]() ,
,
∴![]() 的取值范围是
的取值范围是![]() .
.


科目:初中数学 来源: 题型:
【题目】如图是本地区一种产品30天的销售图像,图1是产品销售量y(件)与时间t(天)的函数关系,图2是一件产品的销售利润z(元)与时间t(天)的函数关系,已知日销售利润=日销售量×每件产品的销售利润,下列结论错误的是( )。
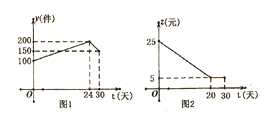
A. 第24天的销售量为200件B. 第10天销售一件产品的利润是15元
C. 第12天与第30天这两天的日销售利润相等D. 第30天的日销售利润是750元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1∥l2∥l3∥l4,相邻两条平行线间的距离均为h,矩形ABCD的四个顶点分别在这四条直线上,放置方式如图所示,AB=4,BC=6,则tanα的值等于( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD中,EF分别是AB、AD边上的点,DE与CF交于点G.
(1)如图1,若四边形ABCD是正方形,且DE⊥CF,求证:DE=CF;

(2)如图2,若四边形ABCD是矩形,且DE⊥CF,求证:![]() ;
;

(3)如图3,若四边形ABCD是平行四边形,当∠B=∠EGF时,第(2)问的结论是否成立?若成立给予证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某市2019年11月21日---11月27日最高气温走势图,则下列说法不正确的是( )

A.21日---22日的最高气温呈上升趋势
B.这7天中,23日的最高气温高于其他6天的的最高气温
C.23---25日的最高气温呈下降趋势
D.相邻两天中,24日---25日的最高气温变化最大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】积极响应市委市政府“加快建设绿水青山的美丽乐山”的号召,我市某街道决定从备选的五种树中选购一种进行栽种.为了更好地了解社情民意,工作人员在街道辖区范围内随机抽取了部分居民,进行“我最喜欢的一种树”的调查活动(每人限选其中一种树),并将调查结果整理后,绘制成如图所示两个不完整的统计图:

请根据所给信息解答以下问题:
(1)这次参与调查的居民人数为______;
(2)请将条形和扇形统计图补充完整;
(3)请计算扇形统计图中“枫树”所在扇形的圆心角度数;
(4)已知该街道辖区内现有居民2万人,请你估计这2万人中最喜欢玉兰树的有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在宽20米,长32米的矩形耕地上,修筑同样宽的三条路(两条纵向,一条横向,并且横向与纵向互相垂直),把这块耕地分成大小相等的六块试验田,要使试验田的面积是570平方米,问道路应该多宽?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() 和
和![]() ,与y轴交于点C.
,与y轴交于点C.
(1)![]() = ,
= ,![]() = ;
= ;
(2)根据函数图象可知,当![]() >
>![]() 时,x的取值范围是 ;
时,x的取值范围是 ;
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当![]() :
:![]() =3:1时,求点P的坐标.
=3:1时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线![]() 与
与![]() 轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线
轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线![]() ,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com