
【题目】已知AB为⊙O的直径,点C为![]() 的中点,BD为弦,CE⊥BD于点E,
的中点,BD为弦,CE⊥BD于点E,



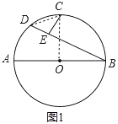
(1)如图1,求证:CE=DE;
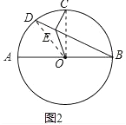
(2)如图2,连接OE,求∠OEB的度数;
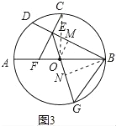
(3)如图3,在(2)条件下,延长CE,交直径AB于点F,延长EO,交⊙O于点G,连接BG,CE=2,EF=3,求△EBG的面积.
【答案】(1)证明见解析;(2)证明见解析;(3)△EBG的面积为6+3![]() .
.
【解析】(1)如图1中,连接CD、OC. 只要证明∠CDE=![]() ∠COB=45°即可.
∠COB=45°即可.
(2)如图2中,连接OD、OC,只要证明△OED≌△OEC,推出∠OED=∠CEO=135°,即可解决问题.
(3)如图3中,过0作OM⊥BD于M,BN⊥EG于N,则∠EMO=90°,连接OC,设EM=x,则BM=DM=2-x,由EF∥OM,得![]() =
=![]() 列出方程即可解决.
列出方程即可解决.
解:(1)证明:如图1中,连接CD、OC.
∵点C是AB![]() 中点,∴AC=BC
中点,∴AC=BC![]() ,∴∠AOC=∠BOC,
,∴∠AOC=∠BOC,
∵∠AOC+∠BOC=180°,∴∠AOC=∠BOC=90°,∴∠D=45°,
∵CE⊥BD,∴∠CED=90°,∴∠D=∠DCE=45°,∴CE=DE.
(2)证明:如图2中,连接OD,OC
在△OED和△OEC中,
OC=OD,CE=DE,OE=OE,
∴△OED≌△OEC,
∵∠CED=90°,∴∠OED=∠CEO=135°,∴∠OEB=45°.
(3)解:如图3中,过O作OM⊥BD于M,BN⊥EG于N,则∠EMO=90°,连接OC.
∵CE=2,∴DE=2,设EM=x,则BM=DM=2+x,∴BE=2x+2,∵∠OEB=45°,则BM=DM=2+x,∴OM=x,
∵∠OEB=45°,∴∠CEB=∠EMO,∴EF∥OM.
∴![]()
![]() ,即
,即![]() ,解得x=2或(
,解得x=2或(![]() 舍去),
舍去),
∴OE=2![]()
![]() ,BM=4,OM=2,BN=3
,BM=4,OM=2,BN=3![]()
![]() ,∴OB=2
,∴OB=2![]()
![]() ∴EG=OE+OG=2
∴EG=OE+OG=2![]()
![]() +2
+2![]()
![]() ,
,
∴S△EBG=![]() EGBN=
EGBN=![]() (2
(2![]()
![]() +2
+2![]()
![]() )×3
)×3![]()
![]() =6+3
=6+3![]()
![]() .
.
“点睛”本题考查圆的综合题、全等三角形的判定和性质、平行线的性质、圆的有关知识,解题的关键是灵活应用这些知识解决问题,学会添加常用辅助线,学会用方程的思想思考问题,属于中考压轴题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】有一种长方体集装箱,其内空长为5米,集装箱截面的高4.5米,宽3.4米,用这样的集装箱运长为5米,横截面的外圆直径为0.8米的圆柱形钢管,为了尽可能多运,排的方案是:圆柱长5米放置于集装箱内空长,圆柱两底面放置于集装箱截面,截面的排法是:
A. 横排,每行分别为4、3、4、3、4、3
B. 横排,每行分别为4、4、4、4、4、3
C. 竖排,每列分别为5、4、5、4、5
D. 竖排,每列分别为5、5、5、5、4
查看答案和解析>>
科目:初中数学 来源: 题型:
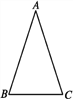
【题目】如图,△ABC是等腰三角形,AB=AC,∠A=36°.
(1)利用尺规作∠B的平分线BD,交AC于点D;(保留作图痕迹,不写作法)
(2)判断△BCD是否为等腰三角形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示:

(1)∵________=__________(已知)
∴AB∥CD(同位角相等,两条直线平行)
(2)∵_________=__________(已知)
∴AB∥CD(内位角相等,两条直线平行)
(3)∵_________+_________=180(已知)
∴AB∥CD(同旁内角互补,两条直线平行)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y与x﹣2成正比例,当x=3时,y=2.
(1)求y与x之间的函数关系式;
(2)当﹣2<x<3时,求y的范围.
(3)证明:△ABC是直角三角形.
(4)请求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了倡导“节约用水,从我做起”,黄冈市政府决定对市直机关500户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中100户家庭一年的月平均用水量(单位:吨).并将调查结果制成了如图所示的条形统计图.
(1)请将条形统计图补充完整;
(2)求这100个样本数据的平均数,众数和中位数;
(3)根据样本数据,估计黄冈市直机关500户家庭中月平均用水量不超过12吨的约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在纸面上有一数轴(如图),折叠纸面.
(1)若1表示的点与-1表示的点重合,则-7表示的点与数__________表示的点重合;
(2)若-1表示的点与8表示的点重合,回答以下问题:
① 12表示的点与数___________表示的点重合;
![]()
② 若数轴上A、B两点之间的距离为2017(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com