
分析 (1)将减法转化为加法,然后按照加法法则计算即可;
(2)利用有理数的加法法则计算即可;
(3)将减法转化为加法,然后按照加法法则计算即可;
(4)将减法转化为加法,然后按照加法法则计算即可;
(5)先将正数和正数相加,负数和负数相加,最后按照加法法则计算;
(6)先将互为相反数的两数相加,然后再按照加法法则计算即可;
(7)先将算式统一为加法运算,然后再按照加法法则计算即可;
(8)先将正数和正数相加,负数和负数相加,最后按照加法法则计算.
解答 解:(1)0-11
=0+(-11)
=-11;
(2)(-13)+(-8)
=-(13+8)
=-21;
(3)(-2)-(-9)
=-2+9
=7;
(4)$-4\frac{1}{2}$-$5\frac{3}{4}$
=-4$\frac{1}{2}$+(-5$\frac{3}{4}$)
=-(4$\frac{1}{2}$+5$\frac{3}{4}$)
=-10$\frac{1}{4}$;
(5)23+(-17)+6+(-22)
=23+6+[(-17)+(-22)]
=29+(-39)
=-10;
(6)(-$\frac{4}{13}$)+(-$\frac{4}{17}$)+$\frac{4}{13}$+(-$\frac{13}{17}$)
=(-$\frac{4}{13}$)+$\frac{4}{13}$+(-$\frac{4}{17}$)+(-$\frac{13}{17}$)
=0+(-1)
=-1;
(7)0-(-6)+2-(-13)-(+8)
=0+6+2+13-8
=13;
(8)-4.2+5.7-8.4+10
=-4.2-8.4+5.7+10
=-12.6+15.7
=3.1.
点评 本题主要考查的是有理数的加减混合运算,掌握有理数的加减运算法则是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,若要建一个长方形鸡场,鸡场的一边靠墙,墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米,围成长方形的鸡场除门之外四周不能有空隙.求:
如图,若要建一个长方形鸡场,鸡场的一边靠墙,墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米,围成长方形的鸡场除门之外四周不能有空隙.求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
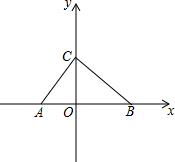 如图所示,点A、B、C的坐标分别为(-$\sqrt{2}$,0),(2$\sqrt{2}$,0),(0,2).
如图所示,点A、B、C的坐标分别为(-$\sqrt{2}$,0),(2$\sqrt{2}$,0),(0,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知A,B两地相距400千米,章老师驾车以80千米/小时的速度从A地到B地.汽车出发前油箱中有油25升,途中加油若干升,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如下图所示.假设汽车每小时耗油量保持不变,以下说法错误的是( )
已知A,B两地相距400千米,章老师驾车以80千米/小时的速度从A地到B地.汽车出发前油箱中有油25升,途中加油若干升,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如下图所示.假设汽车每小时耗油量保持不变,以下说法错误的是( )| A. | 加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系是y=-8t+25 | |
| B. | 途中加油21升 | |
| C. | 汽车加油后还可行驶4小时 | |
| D. | 汽车到达B地时油箱中还余油6升 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com