
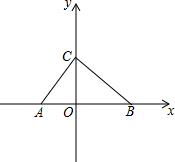
 如图所示,点A、B、C的坐标分别为(-$\sqrt{2}$,0),(2$\sqrt{2}$,0),(0,2).
如图所示,点A、B、C的坐标分别为(-$\sqrt{2}$,0),(2$\sqrt{2}$,0),(0,2).分析 (1)先求得AB、OC的长,然后再计算三角形的面积;
(2)向左平移$\sqrt{2}$个单位,各点的横坐标减$\sqrt{2}$,纵坐标不变.
解答 解:(1)AB=2$\sqrt{2}$-($\sqrt{2}$)=3$\sqrt{2}$,CO=2,
△ABC的面积=$\frac{1}{2}×3\sqrt{2}×2$=3$\sqrt{2}$;
(2)将三角形向左平移$\sqrt{2}$个单位,各点的横坐标减$\sqrt{2}$,纵坐标不变,
此时各点的坐标为A(-2$\sqrt{2}$,0)、B($\sqrt{2}$,0)、C(-$\sqrt{2}$,2).
点评 本题主要考查的是平移与坐标变换,根据各点的坐标求得三角形的底边和高的长度,熟记平移坐标变化的规律是解题的关键.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
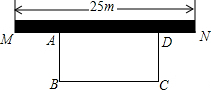 如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在欲砌50m长的墙,砌成一个面积300m2的矩形花园,则BC的长为20 m.
如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在欲砌50m长的墙,砌成一个面积300m2的矩形花园,则BC的长为20 m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
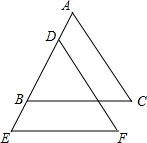 已知:如图BC∥EF,BC=EF,AB=DE;说明AC与DF相等.
已知:如图BC∥EF,BC=EF,AB=DE;说明AC与DF相等.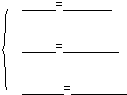
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com