
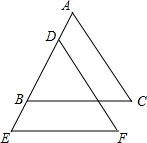
 已知:如图BC∥EF,BC=EF,AB=DE;说明AC与DF相等.
已知:如图BC∥EF,BC=EF,AB=DE;说明AC与DF相等.
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
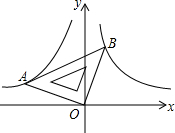 如图,一块等腰直角三角板AOB的直角顶点O与坐标原点生命,点B、A分别在第一、二象限,反比例函数y=$\frac{{k}_{1}}{x}$、y=$\frac{{k}_{2}}{x}$的图象分别经过点A、B,若点A的坐标是(-3,1),分别求出k1,k2的值.
如图,一块等腰直角三角板AOB的直角顶点O与坐标原点生命,点B、A分别在第一、二象限,反比例函数y=$\frac{{k}_{1}}{x}$、y=$\frac{{k}_{2}}{x}$的图象分别经过点A、B,若点A的坐标是(-3,1),分别求出k1,k2的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
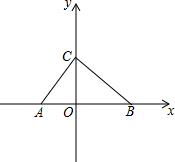 如图所示,点A、B、C的坐标分别为(-$\sqrt{2}$,0),(2$\sqrt{2}$,0),(0,2).
如图所示,点A、B、C的坐标分别为(-$\sqrt{2}$,0),(2$\sqrt{2}$,0),(0,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
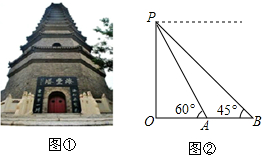 海丰塔是无棣灿烂文化的象征(如图①),喜爱数学实践活动的小伟查资料得知:海丰塔,史称唐塔,原名大觉寺塔,始建于唐贞观十三年(公元639年),碑记为“尉迟敬德监建”,距今已1300多年,被誉为冀鲁三胜之一.小伟决定用自己所学习的知识测量海丰塔的高度.如图②,他利用测角仪站在B处测得海丰塔最高点P的仰角为45°,又前进了18米到达A处,在A处测得P的仰角为60°.请你帮助小伟算算海丰塔的高度.(测角仪高度忽略不计,$\sqrt{3}$≈1.7,结果保留整数).
海丰塔是无棣灿烂文化的象征(如图①),喜爱数学实践活动的小伟查资料得知:海丰塔,史称唐塔,原名大觉寺塔,始建于唐贞观十三年(公元639年),碑记为“尉迟敬德监建”,距今已1300多年,被誉为冀鲁三胜之一.小伟决定用自己所学习的知识测量海丰塔的高度.如图②,他利用测角仪站在B处测得海丰塔最高点P的仰角为45°,又前进了18米到达A处,在A处测得P的仰角为60°.请你帮助小伟算算海丰塔的高度.(测角仪高度忽略不计,$\sqrt{3}$≈1.7,结果保留整数).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com