练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在边长为1的小正方形网格中，点A，B，C均落在格点上．

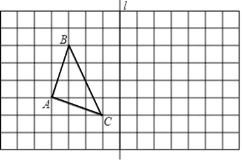
    （1）直接写出△ABC的面积 .

    （2）画出△ABC关于直线的轴对称图形△A1B1C1．

    （3）判断△A1B1C1的形状，并说明理由.

    【答案】（1）5；（2）详见解析；（3）△A1B1C1是等腰直角三角形，理由详见解析.

    【解析】

    （1）利用割补法，即可求得.

    （2）分别作出点A、B、C关于直线l的对称点，再顺次连接即可.

    （3）利用三角形全等即可证得△A1B1C1是等腰直角三角形.

    （1）5

    （2）如图,△A1B1C1即为所求

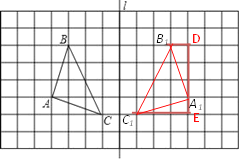
    （3）△A1B1C1是等腰直角三角形.理由如下：

    如图，在△A1B1D和△C1A1E中，

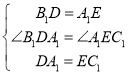
    ∴△A1B1D≌△C1A1E (SAS)

    ∴A1B1=A1C1,∠DA1B1=∠EC1A1

    ∵∠EC1A1+∠C1A1E=90°

    ∴∠DA1B1+∠C1A1E=90°

    ∴∠B1A1C1=180°—（∠DA1B1+∠C1A1E）=90°

    ∴ △A1B1C1是等腰直角三角形

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，AB是半圆O的直径，C是的中点，D是的中点，AC与BD相交于点E.

    （1）求证：BD平分∠ABC；

    （2）求证：BE=2AD；

    （3）求的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】红红有5张写着以下数字的卡片，请你按要求抽出卡片，解决下列问题：

    （1）从中取出2张卡片，使这2张卡片上的数字相乘的积最大，最大值是________.

    （2）从中取出2张卡片，使这2张卡片上的数字相除的商最小，最小值是________.

    （3）从中取出0以外的4张卡片，将这4个数字进行加、减、乘、除或乘方等混合运算，使结果为24，（注：每个数字只能对用一次，如）请另写出两种符合要求的运算式子.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在△ABC中，D是边AB上一点，E是边AC的中点，作CF∥AB交DE的延长线于点F．

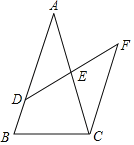
    （1）证明：△ADE≌△CFE；

    （2）若AB＝AC，DB＝2，CE＝5，求CF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将正方形 ABCD （如图 1）作如下划分：

    第1次划分：分别连接正方形ABCD对边的中点（如图2），得线段HF和EG，它们交于点M，此时图2中共有5个正方形；

    第2次划分：将图2 左上角正方形AEMH再作划分，得图3，则图3 中共有9个正方形；

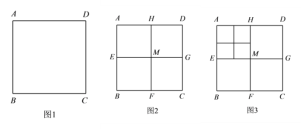
    （1）若每次都把左上角的正方形依次划分下去，则第100次划分后，图中共有 个正方形；

    （2）继续划分下去，第几次划分后能有805个正方形?写出计算过程．

    （3）按这种方法能否将正方形ABCD划分成有2015个正方形的图形？如果能，请算出是第几次划分，如果不能，需说明理由．

    （4）如果设原正方形的边长为1，通过不断地分割该面积为1的正方形，并把数量关系和几何图形巧妙地结合起来，可以很容易得到一些计算结果，试着探究求出下面表达式的结果吧．

    计算 ．（ 直接写出答案即可）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两位同学在一次用频率估计概率的试验中，统计了某一结果出现的频率，给出的 统计图如图所示，则符合这一结果的试验可能是 （ ）

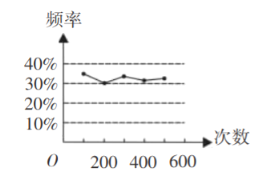
    A.掷一枚硬币，出现正面朝上的概率

    B.掷一枚硬币，出现反面朝上的概率

    C.掷一枚骰子，出现 点的概率

    D.从只有颜色不同的两个红球和一个黄球中，随机取出一个球是黄球的概率

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】背景知识：

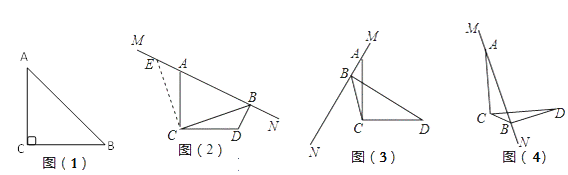
    如图（2），在Rt△ABC中，∠ACB=90°，，则：.

    （1）解决问题：

    如图（2），∠ACD = 90°，AC = DC,MN是过点A的直线，过点D作DB⊥MN于点B，连接CB，试探究线段BA、BC、BD之间的数量关系.

    不妨过点C作CE⊥CB,与MN交于点E，易发现图中出现了一对全等三角形，即 ≌ ，由此可得线段BA、BC、BD之间的数量关系是: .

    （2）类比探究：

    将图（2）中的MN绕点A旋转到图（3）的位置，其它条件不变，试探究线段BA、BC、BD之间的数量关系，并证明.

    （3）拓展应用：

    将图（2）中的MN绕点A旋转到图（4）的位置，其它条件不变，若BD=2，BC=，则AB的长为 .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解密数学魔术：魔术师请观众心想一个数，然后将这个数按以下步骤操作：

    魔术师能立刻说出观众想的那个数．

    (1)如果小玲想的数是-1，那么她告诉魔术师的结果应该是　 　；

    (2)如果小明想了一个数计算后，告诉魔术师结果为93，那么魔术师立刻说出小明想的那个数是　 　；

    (3)观众又进行了几次尝试，魔术师都能立刻说出他们想的那个数．若设观众心想的数为a，请通过计算解密这个魔术的奥妙．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，是的平分线，是的平分线．

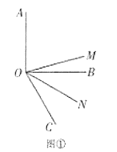
    （1）如图①，当是直角，时，__________，__________，__________；

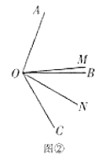
    （2）如图②，当，时，猜想：的度数与的数量关系，并说明理由；

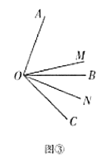
    （3）如图③，当，（为锐角）时，猜想：的度数与，有怎样的数量关系？请写出结论，并说明理由．

    查看答案和解析>>

    同步练习册答案