【题目】如图，在平面直角坐标系中，抛物线y=x2+bx+c与x轴交于点A（﹣1，0），B（3，0），与y轴交于点C，作直线BC，点P是抛物线上一个动点（点P不与点B，C重合），连结PB，PC，以PB，PC为边作CPBD，设CPBD的面积为S，点P的横坐标为m．

（1）求抛物线对应的函数表达式；

（2）当点P在第四象限，且CPBD有两个顶点在x轴上时，求点P的坐标；

（3）求S与m之间的函数关系式；

（4）当x轴将CPBD的面积分成1：7两部分时，直接写出m的值．

参考答案：

【答案】（1）y=x2﹣2x﹣3；（2）（2，﹣3）； （3）S=3m2﹣9m；

（4）m的值为1或1+或1﹣．

【解析】试题分析：（1）利用交点式求抛物线的解析式；

（2）先确定点D在x轴上，再利用平行四边形的性质可判断PC∥x轴，然后根据抛物线的对称性确定点P的坐标；

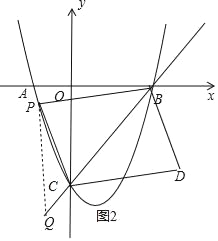
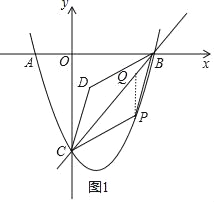
（3）作PQ∥y轴交直线BC于Q，如图1，利用待定系数法求出直线BC的解析式为y=x-3，设P（m，m2-2m-3），则Q（m，m-3），讨论：当0<m<3时，如图1，PQ=-m2+3m，利用三角形面积公式和平行四边形的性质得S=2S△PBC=2（S△PQC+S△PQB）=-3m2+9m；当m<0或m>3时，如图2，PQ=m2-3m，同理可得S=2S△PBC=2（S△PBQ-S△PQC）=3m2-9m；

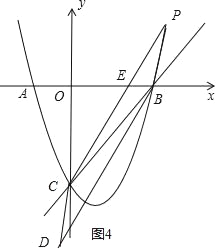
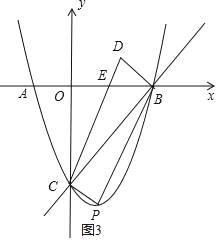
（4）讨论：当点P在x轴下方，如图3，CD交x轴于E，利用已知条件得到S△DEB：S平行四边形CPBD=1：8，再根据平行四边形的性质得S△DEB：S△BCE=1：3，接着根据三角形面积公式得到D点的纵坐标为1，然后利用点平移的坐标规律得到点C向下平移1个单位可得到P点，即P点的纵坐标为-4，则解方程x2-2x-3=-4可得到对应m的值；当点P在x轴上方，如图4，CP交x轴于E，同理可得点P到x轴的距离为1，即P点的纵坐标为1，则通过解方程x2-2x-3=1可得对应m的值．

解：（1）抛物线的解析式为y=（x+1）（x﹣3），

即y=x2﹣2x﹣3；

（2）∵CPBD有两个顶点在x轴上，

∴点D在x轴上，

而BD∥PC，

∴点P和点C为抛物线上的对称点，

而抛物线的对称轴为直线x=1，

∴点P的坐标为（2，﹣3）；

（3）作PQ∥y轴交直线BC于Q，如图1，

设直线BC的解析式为y=kx+b，

把C（0，﹣3），B（3，0）代入得，解得，

∴直线BC的解析式为y=x﹣3，

设P（m，m2﹣2m﹣3），则Q（m，m﹣3），

当0＜m＜3时，如图1，PQ=m﹣3﹣（m2﹣2m﹣3）=﹣m2+3m

S=2S△PBC=2（S△PQC+S△PQB）=23（﹣m2+3m）=﹣3m2+9m；

当m＜0或m＞3时，如图2，PQ=m2﹣2m﹣3﹣（m﹣3）=m2﹣3m

S=2S△PBC=2（S△PBQ﹣S△PQC）=23（m2﹣3m）=3m2﹣9m；

（4）当点P在x轴下方，如图3，CD交x轴于E，

∵x轴将CPBD的面积分成1：7两部分，

∴S△DEB：S平行四边形CPBD=1：8，

∴S△DEB：S△BCD=1：4，

∴S△DEB：S△BCE=1：3，

而OC=3，

∴点D到x轴的距离为1，即D点的纵坐标为1，

∵四边形CPBD为平行四边形，

∴点C向下平移1个单位可得到P点，即P点的纵坐标为﹣4，

当x=﹣4时，x2﹣2x﹣3=﹣4，解得x1=x2=1，则P点坐标为（1，﹣4），

∴m=1；

当点P在x轴上方，如图4，CP交x轴于E，

∵x轴将CPBD的面积分成1：7两部分，

∴S△PEB：S平行四边形CPBD=1：8，

∴S△PEB：S△BCP=1：4，

∴S△PEB：S△BCE=1：3，

而OC=3，

∴点P到x轴的距离为1，即P点的纵坐标为1，

当y=1时，x2﹣2x﹣3=1，解得x1=1+，x2=1﹣，则P点坐标为（1+，1）或（1﹣，1），

∴m=1+或m=1﹣，

综上所述，m的值为1或1+或1﹣．

关闭