

分析 (1)作辅助线,如图1,根据同角的三角函数:cos∠DAB=cos∠COB=$\frac{3}{5}$,设CG=3x,OC=5x,表示AD=AG=9x,根据角平分线的性质得:$\frac{AF}{OF}=\frac{DF}{OF}$=$\frac{9}{5}$,再证明△ADF∽△COF,列比例式可得结论;
(2)如图2,作辅助线,同理根据$\frac{CD}{AD}=\frac{3}{4}$,设CD=3x,AD=4x,则AC=5x,在直角△OCG中根据勾股定理列方程求出半径OC的长,即可表示出tan∠ADO=tan∠DOC的值;
(3)同理设AD=4x,AC=5x,则DC=3x,在Rt△CDP中,求出tan∠BDC的值;
(4)如图4,同理作辅助线,根据角平分线性质设AO=2x,AD=3x,则AP=AD=3x,或利用相似设未知数,由勾股定理和相似表示OC和CG的长,代入三角函数式即可.
解答 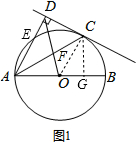 解:(1)如图1,过C作CG⊥AB于G,连接OC,
解:(1)如图1,过C作CG⊥AB于G,连接OC,
∵DC为⊙O的切线,
∴OC⊥CD,
∵AD⊥CD,
∴AD∥OC,
∴∠COB=∠DAB,
∴cos∠DAB=cos∠COB=$\frac{3}{5}$,
设CG=3x,OC=5x,
由勾股定理得:OG=4x,
∵OA=OC,
∴OA=5x,∠OAC=∠ACO,
∵AD∥OC,
∴∠DAC=∠ACO,
∴∠DAC=∠OAC,
∵∠ADC=∠AGC=90°,AC=AC,
∴△ADC≌△AGC,
∴AD=AG=AO+OG=5x+4x=9x,
∵OF平分∠DAB,
∴$\frac{AD}{AO}=\frac{DF}{OF}=\frac{9x}{5x}=\frac{9}{5}$,
∵∠AFD=∠OFC,
∠DAC=∠ACO,
∴△ADF∽△COF,
∴$\frac{AF}{CF}=\frac{DF}{OF}$=$\frac{9}{5}$;
(2)如图2, 过C作CG⊥AB于G,连接AC、OC,
过C作CG⊥AB于G,连接AC、OC,
∵$\frac{CD}{AD}=\frac{3}{4}$,
设CD=3x,AD=4x,则AC=5x,
∵∠DAC=∠CAB,
∴CD=CG=3x,
则AG=4x,
设OC=a,OA=a,则OG=4x-a,
由勾股定理得:a2=(3x)2+(4x-a)2,
a=$\frac{25}{8}$x,
在Rt△OCG中,∴tan∠ADO=tan∠DOC=$\frac{DC}{CO}$=$\frac{3x}{\frac{25}{8}x}$=$\frac{24}{25}$;
(3)∵cos∠CAD=$\frac{4}{5}$=$\frac{AD}{AC}$,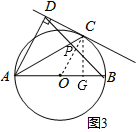
设AD=4x,AC=5x,则DC=3x,
过C作CG⊥AB于G,连接OC,
则CG=DC=3x,AG=4x,
同理得:AO=OC=$\frac{25}{8}$x,
由(1)得:OC∥AD,OA=OC,
∴DP=BP,
∴OP是△ADB的中位线,
∴OP=$\frac{1}{2}$AD=2x,
∴PC=$\frac{25}{8}$x-2x=$\frac{9}{8}$x,
在Rt△CDP中,tan∠BDC=$\frac{PC}{DC}$=$\frac{\frac{9}{8}x}{3x}$=$\frac{3}{8}$;
(4)如图4,过C作CP⊥AB于P,连接OC,
由(1)得:AC平分∠DAO,
∴$\frac{AO}{AD}=\frac{OF}{DF}$,
∵$\frac{OF}{DF}=\frac{2}{3}$,
∴$\frac{AO}{AD}=\frac{2}{3}$,
设AO=2x,AD=3x,则AP=AD=3x,
∴OC=2x,OP=x,
由勾股定理得:CP=$\sqrt{3}$x,
∴CD=CP=$\sqrt{3}$x,
∴OC∥AD,
∴△OCG∽△ADG,
∴$\frac{CO}{AD}=\frac{CG}{DG}$,
∴$\frac{2x}{3x}=\frac{CG}{CG+\sqrt{3}x}$,
∴CG=2$\sqrt{3}$x,
在Rt△OCG中,tan∠G=$\frac{OC}{CG}$=$\frac{2x}{2\sqrt{3}x}$=$\frac{\sqrt{3}}{3}$.
点评 本题是圆的综合题,考查了圆周角定理、三角函数、勾股定理、相似三角形的性质和判定、切线的性质等知识,运用了类比的方法,四个问题中,条件和结论交换,利用三角函数的比例式设未知数,找等量关系式求出未知数,使问题得以解决.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -|-2|=2 | B. | (6.4×106)÷(8×103)=800 | ||
| C. | (-1)2015-12016=-2 | D. | $-6÷({\frac{1}{3}-\frac{1}{2}})=36$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
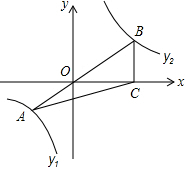 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y1=$\frac{4}{x}$(x<0)图象上一点,AO的延长线交函数y2=$\frac{{k}^{2}}{x}$ (x>0,k<0)的y2图象于点B,BC⊥x轴,若S△ABC=$\frac{15}{2}$,求函数y2.
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y1=$\frac{4}{x}$(x<0)图象上一点,AO的延长线交函数y2=$\frac{{k}^{2}}{x}$ (x>0,k<0)的y2图象于点B,BC⊥x轴,若S△ABC=$\frac{15}{2}$,求函数y2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知Rt△DEF按如图所示的位置放置,∠E=90°,∠EDF=30°,DE=6$\sqrt{3}$,点H为线段FD延长线上一动点,现将△DEH绕点D顺时针旋转60°得到△DAK,E的对应点是A,H的对应点是K,若△EHK的面积为4$\sqrt{3}$,则DH的值为2.
已知Rt△DEF按如图所示的位置放置,∠E=90°,∠EDF=30°,DE=6$\sqrt{3}$,点H为线段FD延长线上一动点,现将△DEH绕点D顺时针旋转60°得到△DAK,E的对应点是A,H的对应点是K,若△EHK的面积为4$\sqrt{3}$,则DH的值为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
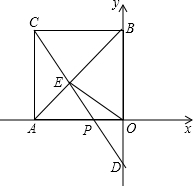 在平面直角坐标系xOy中,四边形OACB是正方形,A点的坐标为(-3,0),点P是射线AO上(异于点A、O)一动点,直线CP与对角线AB及y轴分别交于点E,D.
在平面直角坐标系xOy中,四边形OACB是正方形,A点的坐标为(-3,0),点P是射线AO上(异于点A、O)一动点,直线CP与对角线AB及y轴分别交于点E,D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com