
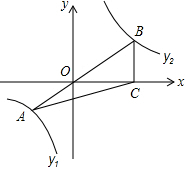
 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y1=$\frac{4}{x}$(x<0)图象上一点,AO的延长线交函数y2=$\frac{{k}^{2}}{x}$ (x>0,k<0)的y2图象于点B,BC⊥x轴,若S△ABC=$\frac{15}{2}$,求函数y2.
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y1=$\frac{4}{x}$(x<0)图象上一点,AO的延长线交函数y2=$\frac{{k}^{2}}{x}$ (x>0,k<0)的y2图象于点B,BC⊥x轴,若S△ABC=$\frac{15}{2}$,求函数y2. 分析 设A(m,$\frac{4}{m}$)(m<0),则可得到直线AB的解析式为y=$\frac{4}{{m}^{2}}$x.再利用反比例函数与一次函数的交点问题可表示出B(-$\frac{1}{2}$mk,-$\frac{2k}{m}$),则利用三角形面积公式得到$\frac{1}{2}$×(-$\frac{2k}{m}$)×(-$\frac{1}{2}$mk+|m|)=$\frac{15}{2}$,解得k1=-5(舍去),k2=3,于是得到y2=$\frac{9}{x}$.
解答 解:设A(m,$\frac{4}{m}$)(m<0),
直线AB的解析式为y=ax(k≠0),
∵A(m,$\frac{4}{m}$),
∴ma=$\frac{4}{m}$,解得a=$\frac{4}{{m}^{2}}$,
∴直线AB的解析式为y=$\frac{4}{{m}^{2}}$x.
∵AO的延长线交函数y=$\frac{{k}^{2}}{x}$的图象于点B,
∴B(-$\frac{1}{2}$mk,-$\frac{2k}{m}$),
∵△ABC的面积等于$\frac{15}{2}$,CB⊥x轴,
∴$\frac{1}{2}$×(-$\frac{2k}{m}$)×(-$\frac{1}{2}$mk+|m|)=$\frac{15}{2}$,解得k1=-5(舍去),k2=3,
∴y2=$\frac{9}{x}$.
点评 本题考查了比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:解答题
| 购物金额(原价) | 优惠率 |
| 不超过3000元的部分 | 无优惠 |
| 超过3000元但不超过10000元部分 | 5% |
| 超过10000元的部分 | 10% |
| 付款时,还可以享受单笔消费满2000元立减160元优惠 | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
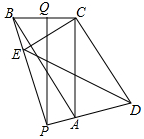 如图,在△ABC中,∠ACB=90°,BC=6,AC=8,将△ABC绕C点旋转一个角度到△DEC,直线AD,EB交于P点,Q是BC的中点,连PQ,在旋转过程中,求:
如图,在△ABC中,∠ACB=90°,BC=6,AC=8,将△ABC绕C点旋转一个角度到△DEC,直线AD,EB交于P点,Q是BC的中点,连PQ,在旋转过程中,求:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
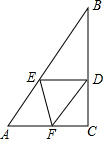 如图,Rt△ABC中,∠C=90°,∠B=30°,点D在BC上,BD=2CD,过D点作BC的垂线交AB于点E,BE=6cm,F为线段AC上一动点,则△DEF的周长最小值为9cm.
如图,Rt△ABC中,∠C=90°,∠B=30°,点D在BC上,BD=2CD,过D点作BC的垂线交AB于点E,BE=6cm,F为线段AC上一动点,则△DEF的周长最小值为9cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD中,∠A=90°,AB=2$\sqrt{5}$,AD=2,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别是DM,MN的中点,则EF长度的最大值为$\sqrt{6}$.
如图,四边形ABCD中,∠A=90°,AB=2$\sqrt{5}$,AD=2,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别是DM,MN的中点,则EF长度的最大值为$\sqrt{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com