
| 购物金额(原价) | 优惠率 |
| 不超过3000元的部分 | 无优惠 |
| 超过3000元但不超过10000元部分 | 5% |
| 超过10000元的部分 | 10% |
| 付款时,还可以享受单笔消费满2000元立减160元优惠 | |
分析 (1)根据优惠政策列式计算即可得出结论;
(2)设实际花费为y元,分0<x<2000、2000≤x≤3000和3000<x≤10000三种情况用含x的代数式表示y值;
(3)分别求出分别支付、冰箱和电视机一起支付洗衣机单独支付、冰箱和洗衣机一起支付电视机单独支付以及电视剧和洗衣机一起支付冰箱单独支付四种情况下的总花费,与(1)的结论比较后即可得出结论.
解答 解:(1)3000+(10000-3000)×(1-5%)+(11500-10000)×(1-10%)-160=10840(元).
答:如果一次性支付,他的实际花费为10840元.
(2)设实际花费为y元.
当0<x<2000时,y=x;
2000≤x≤3000时,y=x-160;
当3000<x≤10000时,y=3000+(x-3000)(1-5%)-160=0.95x-10.
∴实际花费y=$\left\{\begin{array}{l}{x(0<x<2000)}\\{x-160(2000≤x≤3000)}\\{0.95x-10(3000<x≤10000)}\end{array}\right.$.
(3)分别支付时的总花费为3000+(4800-3000)×(1-5%)-160+3000+(4600-3000)(1-5%)-160+2100-160=10850(元);
冰箱和电视机一起支付,洗衣机单独支付时的总花费为3000+(4800+4600-3000)×(1-5%)-160+2100-160=10860(元);
冰箱和洗衣机一起支付,电视机单独支付时的总花费为
3000+(4800+2100-3000)×(1-5%)-160+3000+(4600-3000)×(1-5%)-160=10905(元);
电视剧和洗衣机一起支付,冰箱单独支付时的总花费为
3000+(4600+2100-3000)×(1-5%)-160+3000+(4800-3000)×(1-5%)-160=10905(元).
∵10840<10850<10860<10905,
∴一次性支付,总花费最低.
点评 本题考查了一次函数应用以及列代数式,解题的关键是:(1)根据优惠政策列式计算;(2)分0<x<2000、2000≤x≤3000和3000<x≤10000三种情况找出y关于x的函数关系式;(3)分别求出分别支付、冰箱和电视机一起支付洗衣机单独支付、冰箱和洗衣机一起支付电视机单独支付以及电视剧和洗衣机一起支付冰箱单独支付四种情况下的总花费.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
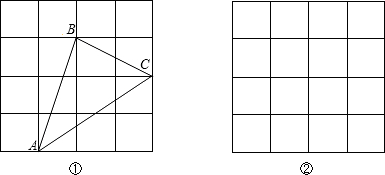
 在如图所示的平面直角坐标系中表示下面各点:A(0,3),B(1,-3),C(3,-5),D(-3,-5),E(3,5),F(5,7),G(5,0).
在如图所示的平面直角坐标系中表示下面各点:A(0,3),B(1,-3),C(3,-5),D(-3,-5),E(3,5),F(5,7),G(5,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
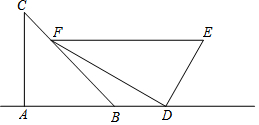 王生是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,A、B、D在同一直线上,EF∥AD,∠A=∠EDF=90°,∠C=45°,∠E=60°,量得DE=4.求:
王生是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,A、B、D在同一直线上,EF∥AD,∠A=∠EDF=90°,∠C=45°,∠E=60°,量得DE=4.求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
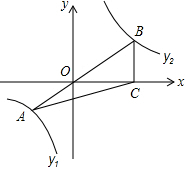 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y1=$\frac{4}{x}$(x<0)图象上一点,AO的延长线交函数y2=$\frac{{k}^{2}}{x}$ (x>0,k<0)的y2图象于点B,BC⊥x轴,若S△ABC=$\frac{15}{2}$,求函数y2.
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y1=$\frac{4}{x}$(x<0)图象上一点,AO的延长线交函数y2=$\frac{{k}^{2}}{x}$ (x>0,k<0)的y2图象于点B,BC⊥x轴,若S△ABC=$\frac{15}{2}$,求函数y2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com