
 如图,四边形ABCD中,∠A=90°,AB=2$\sqrt{5}$,AD=2,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别是DM,MN的中点,则EF长度的最大值为$\sqrt{6}$.
如图,四边形ABCD中,∠A=90°,AB=2$\sqrt{5}$,AD=2,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别是DM,MN的中点,则EF长度的最大值为$\sqrt{6}$. 分析 根据三角形中位线定理可知EF=$\frac{1}{2}$DN,求出DN的最大值即可
解答  解:如图,连结DN,
解:如图,连结DN,
∵DE=EM,FN=FM,
∴EF=$\frac{1}{2}$DN,
当点N与点B重合时,DN的值最大即EF最大,
在Rt△ABD中,
∵∠A=90°,AD=2,AB=2$\sqrt{5}$,
∴BD=$\sqrt{A{D}^{2}+A{B}^{2}}$=2$\sqrt{6}$,
∴EF的最大值=$\frac{1}{2}$BD=$\sqrt{6}$.
故答案为:$\sqrt{6}$.
点评 本题考查三角形中位线定理、勾股定理等知识,解题的关键是中位线定理的灵活应用,学会转化的思想,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
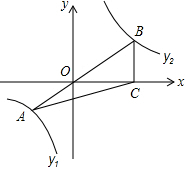 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y1=$\frac{4}{x}$(x<0)图象上一点,AO的延长线交函数y2=$\frac{{k}^{2}}{x}$ (x>0,k<0)的y2图象于点B,BC⊥x轴,若S△ABC=$\frac{15}{2}$,求函数y2.
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y1=$\frac{4}{x}$(x<0)图象上一点,AO的延长线交函数y2=$\frac{{k}^{2}}{x}$ (x>0,k<0)的y2图象于点B,BC⊥x轴,若S△ABC=$\frac{15}{2}$,求函数y2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,3) | B. | (2,-3) | C. | (-2,3) | D. | (-2,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为测量塔的高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是45°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是40m,根据以上观测数据,求观光塔CD的高度.
为测量塔的高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是45°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是40m,根据以上观测数据,求观光塔CD的高度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,甲、乙、丙、丁四个扇形的面积之比是1:2:3:4,则甲、乙、丙、丁四个扇形中圆心角度数最大的是( )度.
如图,甲、乙、丙、丁四个扇形的面积之比是1:2:3:4,则甲、乙、丙、丁四个扇形中圆心角度数最大的是( )度.| A. | 36 | B. | 72 | C. | 144 | D. | 156 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
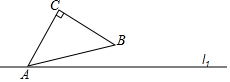 点c是直线l1外一定点,点A是直线l1上一动点,以AC为腰作等腰直角三角形ABC(点B在点C的右侧),当点A在直线l1上运动时,请画出点B的轨迹.
点c是直线l1外一定点,点A是直线l1上一动点,以AC为腰作等腰直角三角形ABC(点B在点C的右侧),当点A在直线l1上运动时,请画出点B的轨迹.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
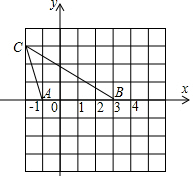 △ABC在平面直角坐标系中的位置如图所示,现另有一点D,满足以A,B,D为顶点的三角形与△ABC全等,则D点坐标为(4,3)或(-2,-3)或(4,-3).
△ABC在平面直角坐标系中的位置如图所示,现另有一点D,满足以A,B,D为顶点的三角形与△ABC全等,则D点坐标为(4,3)或(-2,-3)或(4,-3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com