
【题目】已知一次函数![]() 的图像与
的图像与![]() 轴、
轴、![]() 轴分别相交于点
轴分别相交于点![]() 、
、![]() ,点
,点![]() 在该函数的图像上,
在该函数的图像上, ![]() 到
到![]() 轴、
轴、![]() 轴的距离分别为
轴的距离分别为![]() 、
、![]() .
.
(![]() )当
)当![]() 为线段
为线段![]() 端点
端点![]() 时,求
时,求![]() 的值.
的值.
(![]() )直接写出
)直接写出![]() 的范围,并求当
的范围,并求当![]() 时点
时点![]() 的坐标.
的坐标.
(![]() )若在线段
)若在线段![]() 上存在无数个
上存在无数个![]() 点,使
点,使![]() (
(![]() 为常数),求
为常数),求![]() 的值.
的值.

【答案】(1)2;(2)![]() ,
, ![]() 或
或![]() ;(3)3.
;(3)3.
【解析】试题分析:(1)对于一次函数解析式,求出A的坐标,即可求出P为A时d1+d2的值;
(2)根据题意确定出d1+d2的范围,设P(m,3m-6),表示出d1+d2,分类讨论m的范围,根据d1+d2=3求出m的值,即可确定出P的坐标;
(3)设P(m,3m-6),表示出d1与d2,由P在线段上求出m的范围,利用绝对值的代数意义表示出d1与d2,代入d1+ad2=6,根据存在无数个点P求出a的值即可.
试题解析:(![]() )由题意得
)由题意得![]() ,当
,当![]() 为
为![]() 时,则
时,则![]() ,
, ![]() ,
,
∴![]() ;
;
(![]() )设
)设![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,
,
∴![]() ,
,
当![]() 时,
时, ![]() ,
,
∴![]() ,
,
综上, ![]() ,当
,当![]() 时,若
时,若![]() ,则
,则![]() ,
, ![]() ,∴
,∴![]() ;
;
当![]() 时,若
时,若![]() ,则
,则![]() ,
, ![]() ,
,
∴![]() ;
;
(![]() )设P(m,2m-4),∴d1=|3m-6|,d2=|m|,
)设P(m,2m-4),∴d1=|3m-6|,d2=|m|,
∵P在线段AB上,
∴0≤m≤2,
∴d1=6-3m,d2=m,
∵d1+ad2=6,
∴6-3m+am=6,即(a-3)m=0,
∵有无数个点,
∴a=3.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】在边长为10的等边![]() 中,点
中,点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 移动,同时点
移动,同时点![]() 从点
从点![]() 出发沿线段
出发沿线段![]() 的延长线移动,点
的延长线移动,点![]() 、
、![]() 移动的速度相同,
移动的速度相同, ![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
(1)如图①,当点![]() 为
为![]() 的中点时,
的中点时,
(I)求证: ![]() ;(II)求
;(II)求![]() 的长;
的长;



(2)如图②,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,当点
,当点![]() 、
、![]() 在移动的过程中,试确定
在移动的过程中,试确定![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古运河是扬州的母亲河,为打造古运河风光带,现有一段长为180米的河道整治任务由A、B两个工程队先后接力完成.A工程队每天整治12米,B工程队每天整治8米,共用时20天.
(1)根据题意,甲、乙两个同学分别列出了尚不完整的方程组如下:
甲: 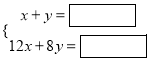 乙:
乙: 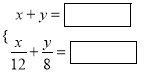
根据甲、乙两名同学所列的方程组,请你分别指出未知数x、y表示的意义,然后在方框中补全甲、乙两名同学所列的方程组:
甲:x表示________,y表示________;
乙:x表示________,y表示________.
(2)求A、B两工程队分别整治河道多少米.(写出完整的解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知直线 AB、CD 相交于点 O,∠COE=90°
(1)若∠AOC=36°,求∠BOE 的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE 的度数.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923292236627968/1924724835590144/STEM/dc8ee683cff64dfdb92368e07f9f9b9d.png]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五段彩虹展翅飞”,横跨南渡江的琼州大桥如图,该桥的两边均有五个红色的圆拱,如图(1).最高的圆拱的跨度为110m,拱高为22m,如图(2),那么这个圆拱所在圆的直径为多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的个数是( )
①射线MN与射线NM是同一条射线;
②两点确定一条直线;
③两点之间直线最短;
④若2AB=AC,则点B是AC的中点
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com