
【题目】已知x=4是关于x的不等式x﹣3m+2≤0的解,则m的取值范围为_____.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:

(1)写出用含x、y的代数式表示厨房的面积是________m2;卧室的面积是________m2;
(2)写出用含x、y的代数式表示这套房的总面积是多少平方米?
(3)当x=3,y=2时,求小王这套房的总面积是多少平方米?
(4)若在(3)中,小王到某商店挑选了80cm×80cm的地砖来镶客厅和卧室,他应买多少块才够用?(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图像与
的图像与![]() 轴、
轴、![]() 轴分别相交于点
轴分别相交于点![]() 、
、![]() ,点
,点![]() 在该函数的图像上,
在该函数的图像上, ![]() 到
到![]() 轴、
轴、![]() 轴的距离分别为
轴的距离分别为![]() 、
、![]() .
.
(![]() )当
)当![]() 为线段
为线段![]() 端点
端点![]() 时,求
时,求![]() 的值.
的值.
(![]() )直接写出
)直接写出![]() 的范围,并求当
的范围,并求当![]() 时点
时点![]() 的坐标.
的坐标.
(![]() )若在线段
)若在线段![]() 上存在无数个
上存在无数个![]() 点,使
点,使![]() (
(![]() 为常数),求
为常数),求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
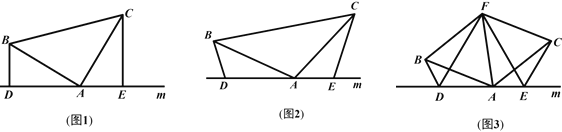
【题目】(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?若成立,请给出证明;若不成立,请说明理由.
(3)拓展与应用:如图3,D、E是D、A、E三点所在直线m上的两动点(D、A、E三点
互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数![]() 的图象与x轴、y轴分别交于点A、B,与函数
的图象与x轴、y轴分别交于点A、B,与函数![]() 图象交于点M,点M的横坐标为2,在x轴上有点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数
图象交于点M,点M的横坐标为2,在x轴上有点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数![]() 和
和![]() 的图象于点C、D.
的图象于点C、D.
(1)求点A的坐标:
(2)若OB=CD,求a的值
(3)在(2)条件下若以0D线段为边,作正方形0DEF,求直线EF的表达式.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学“综合与实践”课中,老师带领同学们来到娄底市郊区,测算如图所示的仙女峰的高度,李红盛同学利用已学的数学知识设计了一个实践方案,并实施了如下操作:先在水平地面A处测得山顶B的仰角∠BAC为38.7°,再由A沿水平方向前进377米到达山脚C处,测得山坡BC的坡度为1:0.6,请你求出仙女峰的高度(参考数据:tan38.7°≈0.8)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com