
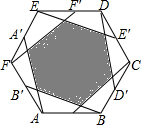
 如图,正六边形ABCDEF的面积为2009,A′至F′为各边中点,顺次连接AA′至FF′,求阴影六边形的面积.
如图,正六边形ABCDEF的面积为2009,A′至F′为各边中点,顺次连接AA′至FF′,求阴影六边形的面积. 分析 设正六边形ABCDEF的边长为2a,作F′M⊥EF于M,则∠M=90°,由正六边形的性质得出∠EF′M=30°,得出EM=$\frac{1}{2}$a,MF′=$\frac{\sqrt{3}}{2}$a,由勾股定理求出FF′,证明△A′FG∽△F′FE,得出对应边成比例$\frac{AG}{EF′}=\frac{FG}{EF}=\frac{A′F}{FF′}$,得出FG=2A′G=2F′H,求出FG=$\frac{2\sqrt{7}}{7}$a,得出GH=FF'-FG-HF'=$\frac{4\sqrt{7}}{7}$a,由阴影正六边形与正六边形ABCDEF的面积比等于相似比的平方,即可得出阴影六边形的面积.
解答 解:设正六边形ABCDEF的边长为2a,
∵A′、F′分别是EF、DE的中点,
∴A′F=EF′=a,
作F′M⊥EF于M,如图所示: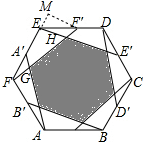
则∠M=90°,
由正六边形的性质得:∠FEF′=120°,
∴∠MEF′=60°,
∴∠EF′M=30°,
∴EM=$\frac{1}{2}$a,MF′=$\frac{\sqrt{3}}{2}$a,
∴FM=$\frac{5}{2}$a,
∴FF′=$\sqrt{F{M}^{2}+MF{′}^{2}}$=$\sqrt{7}$a,
由题意得:阴影六边形是正六边形,
∴∠A′GF=120°=∠FED,
又∵∠A′FG=∠F′FE,
∴△A′FG∽△F′FE,
∴$\frac{AG}{EF′}=\frac{FG}{EF}=\frac{A′F}{FF′}$,
∴FG=2A′G=2F′H,$\frac{FG}{2a}=\frac{a}{\sqrt{7}a}$,
解得:FG=$\frac{2\sqrt{7}}{7}$a,
∴GH=FF'-FG-HF'=FF'-$\frac{3}{2}$FG=$\frac{4\sqrt{7}}{7}$a,
∵阴影正六边形∽正六边形ABCDEF,
∴阴影正六边形的面积:正六边形ABCDEF的面积=($\frac{4\sqrt{7}}{7}$a:2a)2=4:7,
∴阴影六边形的面积=$\frac{4}{7}$×2009=1148.
点评 本题考查了正六边形的性质、勾股定理,三角函数、相似三角形的判定与性质、含30°角的直角三角形的性质等知识;本题综合性强,难度较大,需要作辅助线运用勾股定理和证明三角形相似才能得出结果.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
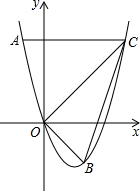 如图,二次函数y=x2+bx的图象经过点A(-1,4)和点B(2,m).
如图,二次函数y=x2+bx的图象经过点A(-1,4)和点B(2,m).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,庄子大桥有一段抛物线形的拱梁,抛物线的表达式为y=ax2+bx,小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁高度相同,则小强骑自行车通过拱梁部分的桥面OC共需( )
如图,庄子大桥有一段抛物线形的拱梁,抛物线的表达式为y=ax2+bx,小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁高度相同,则小强骑自行车通过拱梁部分的桥面OC共需( )| A. | 18秒 | B. | 36秒 | C. | 38秒 | D. | 46秒 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知AB=AC,AD=AE,∠BAC=∠DAE,直线BD、CE交于点G,
已知AB=AC,AD=AE,∠BAC=∠DAE,直线BD、CE交于点G,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com