Question

1．如图，Rt△ABC中，∠ACB=90°．
（1）分别以AB，AC为边向外作等边三角形ABD和等边三角形ACE，连接CE交AB于点F，若∠BAC=30°，求证：DF=EF；
（2）分别以AB，AC为底边向形外作等腰三角形ABD和等腰三角形ACE，且∠ADB=∠AEC=2∠BAC=2α，用含α的锐角三角函数表示EF与DF的数量关系．

Answer 1

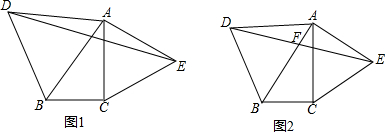
分析 （1）如图1，取AB的中点G，连接DG，EG，根据等边三角形和直角三角形的性质推出△ABC≌△EGA，由全等三角形的性质得到GE=AB，根据等边三角形的性质得到AD=EG，证得AD∥EG，推出四边形ADGE是平行四边形，根据平行四边形的性质即可得到结论；
（2）先过点E作EH⊥AC，延长交AB于G，连接DG，得出AH=CH，EH⊥AC，根据∠BCA=90°，证出GH∥BC，AG=BG，再根据AD=BD，得出DG⊥AB，最后根据AD⊥AC，AE⊥AB，得出GE∥AD，DG∥AE，从而证出四边形ADGE是平行四边形，即可求出答案．

解答 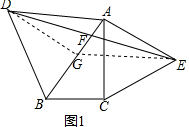解：（1）如图1，取AB的中点G，连接DG，EG，
∵△ACE是等边三角形，
∴∠EAC=60°，AE=AC，
∵∠BAC=30°，
∴∠GAE=∠ACB=90°，AB=2BC，
∵G为AB的中点，
∴AB=2AG，
∴BC=AG，
在△ABC与△EGA中，$\left\{\begin{array}{l}{BC=AG}\\{∠GAE=∠ACB}\\{AC=AE}\end{array}\right.$，
∴△ABC≌△EGA，
∴GE=AB，
∵△ADB是等边三角形，
∴AD=AB，
∴AD=EG，
∵∠DAB=∠EAC=60°，∠BAC=∠AEG=30°，
∴AD⊥AC，EG⊥AC，∴AD∥EG，
∴四边形ADGE是平行四边形，
∴DF=EF；

（2）过点E作EH⊥AC，延长交AB于G，连接DG，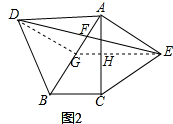
∵AE=EC，
∴AH=CH，EH⊥AC，
∵∠BCA=90°，
∴GH∥BC，
∴AG=BG，
∵AD=BD，
∴DG⊥AB，
∵AD⊥AC，AE⊥AB，
∴GE∥AD，DG∥AE，
∴四边形ADGE是平行四边形，
∴DF=EF，
∵DG∥AE，
∴△DGF∽△AEF，∠EAF=90°，
∴$\frac{DF}{EF}$=$\frac{DG}{AE}$=$\frac{AG}{tanα}$：$\frac{AH}{sinα}$，
∴$\frac{DF}{EF}$=$\frac{AG}{AH}$•$\frac{tanα}{sinα}$=$\frac{tanα}{cosαsinα}$．

点评 本题考查了平行四边形的判定和性质，全等三角形的判定和性质，等边三角形的性质，直角三角形的性质，正确的作出辅助线是解题的关键．