
| A. | 等腰三角形 | B. | 直角三角形 | ||
| C. | 等边三角形 | D. | 等边三角形或直角三角形 |
分析 根据a2+ab-ac-bc=b2+bc-ba-ca=0得到a2+ab-ac-bc=0,b2+bc-ba-ca=0,然后连续提取公因式即可得到(a+b)(a-c)=0,(b+c)(b-a)=0,再根据a+b≠0,b+c≠0得到a-c=0,b-a=0,从而得到a=c,b=a,得到该三角形为等边三角形.
解答 解:∵a2+ab-ac-bc=b2+bc-ba-ca=0,
∴a2+ab-ac-bc=0,b2+bc-ba-ca=0,
∴a(a+b)-c(a+b)=0,b(b+c)-a(b+c)=0
(a+b)(a-c)=0,(b+c)(b-a)=0
∵a+b≠0,b+c≠0,
∴a-c=0,b-a=0
∴a=c,b=a,
∴该三角形是等边三角形.
故选C.
点评 本题考查了因式分解的应用,解题的关键是能够对题目提供的式子进行因式分解,难度不大.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
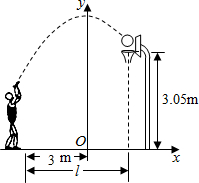 如图,小姚身高$\frac{9}{4}$m在某次投篮中,球的运动路线是抛物线y=-$\frac{1}{5}$x2+$\frac{7}{2}$的一部分,若命中篮圈中心,则他与篮底的距离是( )
如图,小姚身高$\frac{9}{4}$m在某次投篮中,球的运动路线是抛物线y=-$\frac{1}{5}$x2+$\frac{7}{2}$的一部分,若命中篮圈中心,则他与篮底的距离是( )| A. | 3.5m | B. | 4m | C. | 4.5m | D. | 4.6m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com