
【题目】如图,矩形ABCD中,AB=16cm,AD=4cm,点P、Q分别从A、B同时出发,点P在边AB上沿AB方向以2cm/s的速度匀速运动,点Q在边BC上沿BC方向以1cm/s的速度匀速运动,当其中一点到达终点时,另一点也随之停止运动.设运动时间为x秒,△PBQ的面积为y(cm2).
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.,并指出此时x的值.

【答案】(1)y=-x2+8x,自变量取值范围0<x≤4;(2)当x=4时,y有最大值,最大值为16.
【解析】
试题(1)根据矩形的对边相等表示出BC,然后表示出PB、QB,再根据三角形的面积列式整理即可得解,根据点Q先到达终点确定出x的取值范围即可;
(2)利用二次函数的最值问题解答.
试题解析:(1)∵四边形ABCD是矩形,
∴BC=AD=4,
根据题意,AP=2x,BQ=x,
∴PB=162x,
∵S△PBQ=![]() PBQB,
PBQB,
∴y=x2+8x,
∵点P的速度是2cm/s,点Q的速度是1cm/s,
∴点P到达终点的时间是16÷2=8秒,
点Q到达终点的时间是4÷1=4秒,
∵一点到达终点时,另一点也随之停止运动,
∴自变量取值范围:0<x4;
(2)∵y=x2+8x=(x4)2+16,
∴当x=4时,y有最大值,最大值为16,
∴△PBQ的面积的最大值为16cm2.


科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() 与
与![]() 交于点
交于点![]() .有下列结论:①
.有下列结论:①![]() ≌
≌![]() ;②
;②![]() ≌
≌![]() ;③点
;③点![]() 在
在![]() 的平分线上;④点
的平分线上;④点![]() 在
在![]() 的中垂线上.以上结论正确的有_________________.(填序号)
的中垂线上.以上结论正确的有_________________.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为直角三角形,∠ACB=900,AC=BC,点A、C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B、D.
(1)求点A的坐标(用m表示);
(2)求抛物线的解析式;
(3)设点Q为抛物线上点P至点B之间的一动点,连结PQ并延长交BC于点E,连结BQ并延长交AC于点F,试证明:FC(AC+BC)为定值. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在八年级开展环保知识问卷调查活动,问卷一共10道题,八年级(三)班的问卷得分情况统计图如下图所示:

(1)扇形统计图中,![]() ______________;
______________;
(2)根据以上统计图中的信息,
①问卷得分的极差是_____________分;②问卷得分的众数是____________分;③问卷得分的中位数是______________分;
(3)请你求出该班同学的平均分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②b<a+c;③4a+2b+c>0;④b2-4ac>0;其中正确的结论有________(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC,如图所示.
(1)求被剪掉阴影部分的面积:
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
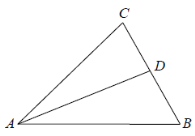
【题目】如图,在![]() 中,
中,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() .
.
(1)尺规作图:作![]() 平分
平分![]() ,分别交
,分别交![]() 于点
于点![]() ;(保留作图痕迹,不必写出作法)
;(保留作图痕迹,不必写出作法)
(2)在(1)的条件下,求证:点![]() 在
在![]() 的平分线上;
的平分线上;
(3)若![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,请画出符合条件的图形,猜想
,请画出符合条件的图形,猜想![]() 和
和![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】石狮泰禾某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“十一”国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)设每件童装降价x元时,每天可销售______ 件,每件盈利______ 元;(用x的代数式表示)
(2)每件童装降价多少元时,平均每天赢利1200元.
(3)要想平均每天赢利2000元,可能吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学课上,老师在屏幕上出示了一个例题:在△ABC中,D,E分别是AB,AC上的一点,BE与CD交于点O,画出图形(如图),给出下列四个条件:①∠DBO=∠ECO;②∠BDO=∠CEO;③BD=CE;④OB=OC.

(1)要求同学从这四个等式中选出两个作为已知条件,可判定△ABC是等腰三角形.
请你用序号在横线上写出所有情形.答:
(2)选择第(1)题中的一种情形,说明△ABC是等腰三角形的理由,并写出解题过程.
解:我选择 .
证明:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com