
【题目】△ABC为等边三角形,边长为a,DF⊥AB.EF⊥AC
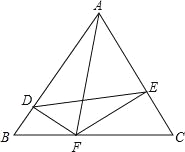
(1)求证:△BDF∽△CEF;
(2)若a=4,设BF=m,四边形ADFE面积为S,求出S与m之间的函数关系式,并探究当m为何值时S取最大值.
【答案】(1)证明见解析;(2)最大值为3![]() .
.
【解析】
试题分析:(1)由等边三角形的性质得出∠B=∠C=60°,由已知得出∠BDF=∠CEF=90°,即可证出△BDF∽△CEF;
(2)作AM⊥BC于M,由等边三角形的性质得出AB=BC=4,BM=CM=![]() BC=2,由勾股定理求出AM,得出△ABC的面积;求出∠DFB=∠EFC=30°,由含30°角的直角三角形的性质得出BD=
BC=2,由勾股定理求出AM,得出△ABC的面积;求出∠DFB=∠EFC=30°,由含30°角的直角三角形的性质得出BD=![]() BF=
BF=![]() m,CE=
m,CE=![]() CF=
CF=![]() (4-m),得出DF、EF的长度,求出△BDF和△CEF的面积,由四边形ADFE面积S=△ABC的面积-△BDF的面积-△CEF的面积,得出S与m之间的函数关系式为S=-
(4-m),得出DF、EF的长度,求出△BDF和△CEF的面积,由四边形ADFE面积S=△ABC的面积-△BDF的面积-△CEF的面积,得出S与m之间的函数关系式为S=-![]() m2+
m2+![]() m+2
m+2![]() ;化成顶点式,得出当m=2时,S取最大值为3
;化成顶点式,得出当m=2时,S取最大值为3![]() 即可.
即可.
试题解析:(1)∵△ABC为等边三角形,
∴∠B=∠C=60°,
∵DF⊥AB.EF⊥AC,
∴∠BDF=∠CEF=90°,
∴△BDF∽△CEF;
(2)作AM⊥BC于M,如图所示:

∵△ABC是等边三角形,
∴AB=BC=4,BM=CM=![]() BC=2,
BC=2,
∴AM=![]() =
=![]() =2
=2![]() ,
,
∴△ABC的面积=![]() BCAM=
BCAM=![]() ×4×2
×4×2![]() =4
=4![]() ,
,
∵BF=m,
∴CF=4-m,
∵∠BDF=∠CEF=90°,∠B=∠C=60°,
∴∠DFB=∠EFC=30°,
∴BD=![]() BF=
BF=![]() m,CE=
m,CE=![]() CF=
CF=![]() (4-m),
(4-m),
∴DF=![]() BD=
BD=![]() m,EF=
m,EF=![]() CE=
CE=![]() (4-m),
(4-m),
∴△BDF的面积=![]() BDDF=
BDDF=![]() ×
×![]() m×
m×![]() m=
m=![]() m2,
m2,
△CEF的面积=![]() CEEF=
CEEF=![]() ×
×![]() (4-m)×
(4-m)×![]() (4-m)=
(4-m)=![]() (4-m)2,
(4-m)2,
∴四边形ADFE面积S=△ABC的面积-△BDF的面积-△CEF的面积=4![]() -
-![]() m2-
m2-![]() (4-m)2=-
(4-m)2=-![]() m2+
m2+![]() m+2
m+2![]() ,
,
即S与m之间的函数关系式为S=-![]() m2+
m2+![]() m+2
m+2![]() ;
;
又∵S=-![]() m2+
m2+![]() m+2
m+2![]() =-
=-![]() (m-2)2+3
(m-2)2+3![]() ,-
,-![]() <0,
<0,
∴当m=2时,S取最大值为3![]() .
.


科目:初中数学 来源: 题型:
【题目】观察下列算式:(﹣2)1=﹣2,(﹣2)2=4,(﹣2)3=﹣8,(﹣2)4=16,(﹣2)5=﹣32,(﹣2)6=64,(﹣2)7=﹣128…通过观察,用你发现的规律写出(﹣2)2016的末位数字是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如下图, AB∥CD,点E,F分别为AB,CD上一点.
(1) 在AB,CD之间有一点M(点M不在线段EF上),连接ME,MF,试探究∠AEM,∠EMF,∠MFC之间有怎样的数量关系. 请补全图形,并在图形下面写出相应的数量关系,选其中一个进行证明.

(2)如下图,在AB,CD之间有两点M,N,连接ME,MN,NF,请选择一个图形写出∠AEM,∠EMN,∠MNF,∠NFC 存在的数量关系(不需证明).
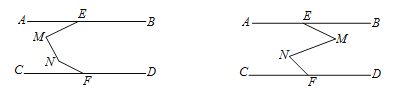
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下三条线段为边,能组成三角形的是( )
A.1cm、2cm、3cm
B.2cm、2cm、4cm
C.3cm、4cm、5 cm
D.4cm、8cm、2cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com