
【题目】我们定义一种新函数:形如![]() (
(![]() ,且
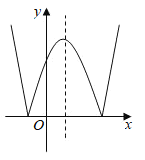
,且![]() )的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2-2x-3|
)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2-2x-3|![]() 的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为
的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为![]() ,
,![]() 和
和![]() ;②图象具有对称性,对称轴是直线
;②图象具有对称性,对称轴是直线![]() ;③当
;③当![]() 或
或![]() 时,函数值
时,函数值![]() 随
随![]() 值的增大而增大;④当
值的增大而增大;④当![]() 或
或![]() 时,函数的最小值是0;⑤当
时,函数的最小值是0;⑤当![]() 时,函数的最大值是4.其中正确结论的个数是______.
时,函数的最大值是4.其中正确结论的个数是______.
【答案】4
【解析】
由![]() ,
,![]() 和
和![]() 坐标都满足函数
坐标都满足函数![]() ,∴①是正确的;从图象可以看出图象具有对称性,对称轴可用对称轴公式求得是直线
,∴①是正确的;从图象可以看出图象具有对称性,对称轴可用对称轴公式求得是直线![]() ,②也是正确的;
,②也是正确的;
根据函数的图象和性质,发现当![]() 或
或![]() 时,函数值
时,函数值![]() 随
随![]() 值的增大而增大,因此③也是正确的;函数图象的最低点就是与
值的增大而增大,因此③也是正确的;函数图象的最低点就是与![]() 轴的两个交点,根据
轴的两个交点,根据![]() ,求出相应的
,求出相应的![]() 的值为
的值为![]() 或
或![]() ,因此④也是正确的;从图象上看,当
,因此④也是正确的;从图象上看,当![]() 或
或![]() ,函数值要大于当
,函数值要大于当![]() 时的
时的![]() ,因此⑤时不正确的;逐个判断之后,可得出答案.
,因此⑤时不正确的;逐个判断之后,可得出答案.
解:①∵![]() ,
,![]() 和
和![]() 坐标都满足函数
坐标都满足函数![]() ,∴①是正确的;
,∴①是正确的;
②从图象可知图象具有对称性,对称轴可用对称轴公式求得是直线![]() ,因此②也是正确的;
,因此②也是正确的;
③根据函数的图象和性质,发现当![]() 或
或![]() 时,函数值
时,函数值![]() 随
随![]() 值的增大而增大,因此③也是正确的;
值的增大而增大,因此③也是正确的;
④函数图象的最低点就是与![]() 轴的两个交点,根据
轴的两个交点,根据![]() ,求出相应的
,求出相应的![]() 的值为
的值为![]() 或
或![]() ,因此④也是正确的;
,因此④也是正确的;
⑤从图象上看,当![]() 或
或![]() ,函数值要大于当
,函数值要大于当![]() 时的
时的![]() ,因此⑤时不正确的;
,因此⑤时不正确的;
故答案是:4
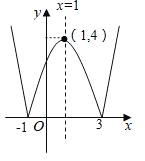


科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
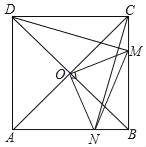
【题目】如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N,连接OM,ON,MN.下列四个结论:①△CNB≌△DMC;②△CON≌△DOM;③△OMN≌△OAD;④AN2+CM2=MN2;其中正确的结论是_____.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 图象的顶点为
图象的顶点为![]() ,对称轴是直线
,对称轴是直线![]() ,一次函数
,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,且与直线
,且与直线![]() 关于
关于![]() 的对称直线交于点
的对称直线交于点![]() .
.
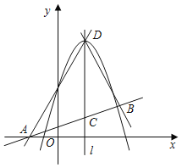
(1)点![]() 的坐标是 ______;
的坐标是 ______;
(2)直线![]() 与直线
与直线![]() 交于点
交于点![]() ,
,![]() 是线段
是线段![]() 上一点(不与点
上一点(不与点![]() 、
、![]() 重合),点
重合),点![]() 的纵坐标为
的纵坐标为![]() .过点
.过点![]() 作直线与线段
作直线与线段![]() 、
、![]() 分别交于点
分别交于点![]() ,
,![]() ,使得
,使得![]() 与
与![]() 相似.
相似.
①当![]() 时,求
时,求![]() 的长;
的长;
②若对于每一个确定的![]() 的值,有且只有一个
的值,有且只有一个![]() 与
与![]() 相似,请直接写出
相似,请直接写出![]() 的取值范围 ______.
的取值范围 ______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划组织240名师生到红色教育基地开展革命传统教育活动.旅游公司有A,B两种客车可供租用,A型客车每辆载客量45人,B型客车每辆载客量30人.若租用4辆A型客车和3辆B型客车共需费用10700元;若租用3辆A型客车和4辆B型客车共需费用10300元.
(1)求租用A,B两型客车,每辆费用分别是多少元;
(2)为使240名师生有车坐,且租车总费用不超过1万元,你有哪几种租车方案?哪种方案最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】央视热播节目“朗读者”激发了学生的阅读兴趣,某校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:
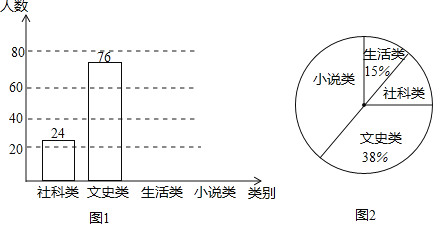
(1)此次共调查了 名学生;
(2)将条形统计图1补充完整;
(3)图2中“小说类”所在扇形的圆心角为 度;
(4)若该校共有学生2000人,估计该校喜欢“社科类”书籍的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
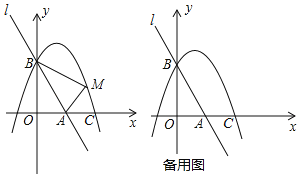
【题目】如图,直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2﹣2ax+a+4(a<0)经过点B,交x轴正半轴于点C.
(1)求该抛物线的函数表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值及此时动点M的坐标;
(3)将点A绕原点旋转得点A′,连接CA′、BA′,在旋转过程中,一动点M从点B出发,沿线段BA′以每秒3个单位的速度运动到A′,再沿线段A′C以每秒1个单位长度的速度运动到C后停止,求点M在整个运动过程中用时最少是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
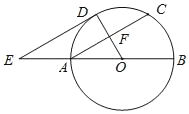
【题目】如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交弧AC于点D,过点D作⊙O的切线,交BA的延长线于点E.
(1)求证:AC∥DE;
(2)连接AD、CD、OC.填空
①当∠OAC的度数为 时,四边形AOCD为菱形;
②当OA=AE=2时,四边形ACDE的面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com