
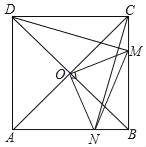
【题目】如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N,连接OM,ON,MN.下列四个结论:①△CNB≌△DMC;②△CON≌△DOM;③△OMN≌△OAD;④AN2+CM2=MN2;其中正确的结论是_____.(填写所有正确结论的序号)
【答案】①②④
【解析】
①易证△CNB≌△DMC(ASA),①正确;②由△CNB≌△DMC得CM=BN,证得△CON≌△DOM(SAS),②正确;③证得△MON是等腰直角三角形,可得△OMN∽△OAD,③不正确;④由勾股定理得在Rt△BMN中,BM2+BN2=MN2,由 AB=BC,CM=BN,推出BM=AN,可得AN2+CM2=MN2,④正确
∵正方形ABCD中,CD=BC,∠BCD=90°,
∴∠BCN+∠DCN=90°,
又∵CN⊥DM,
∴∠CDM+∠DCN=90°,
∴∠BCN=∠CDM,
在△CNB和△DMC中, ,
,
∴△CNB≌△DMC(ASA),①正确;
∴CM=BN,
∵四边形ABCD是正方形,
∴∠OCM=∠OBN=45°,OC=OB=OD,
在△OCM和△OBN中, ,
,
∴△OCM≌△OBN(SAS),
∴OM=ON,∠COM=∠BON,
∴∠DOC+∠COM=∠COB+∠BPN,即∠DOM=∠CON,
在△CON和△DOM中, ,
,
∴△CON≌△DOM(SAS),②正确;
∵∠BON+∠BOM=∠COM+∠BOM=90°,
∴∠MON=90°,即△MON是等腰直角三角形,
又∵△AOD是等腰直角三角形,
∴△OMN∽△OAD,③不正确;
∵AB=BC,CM=BN,
∴BM=AN,
![]()
![]() ,④正确;
,④正确;
故答案为:①②④.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如果抛物线y=-x2+bx+c经过A(0,-2),B(-1,1)两点,那么此抛物线经过
A. 第一、二、三、四象限 B. 第一、二、三象限
C. 第一、二、四象限 D. 第二、三、四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
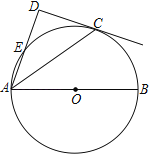
【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
(1)求证:AC平分∠DAB;
(2)连接BC,若cos∠CAD=![]() ,⊙O的半径为5,求CD、AE的值.
,⊙O的半径为5,求CD、AE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)判断以O,A1,B为顶点的三角形的形状.(无须说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
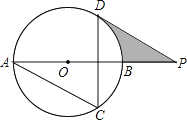
【题目】如图,AB是⊙O的直径,AC,DC是⊙O的两条弦,点P在AB的延长线上.已知,∠ACD=60°,∠APD=30°
(1)求证:PD是⊙O的切线;
(2)若AB=4,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣5(a≠0)与x轴交于点A(﹣5,0)和点B(3,0),与y轴交于点C.
(1)求该抛物线的解析式;
(2)若点E为x轴下方抛物线上的一动点,当S△ABE=S△ABC时,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在点P,使∠BAP=∠CAE?若存在,求出点P的横坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 为锐角
为锐角![]() 内部一点,过点
内部一点,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,以
,以![]() 为直径作
为直径作![]() ,交直线
,交直线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() .
.
(2)连接![]() ,当
,当![]() ,
,![]() 时,在点
时,在点![]() 的整个运动过程中.
的整个运动过程中.
①若![]() ,求
,求![]() 的长.
的长.
②若![]() 为等腰三角形,求所有满足条件的
为等腰三角形,求所有满足条件的![]() 的长.
的长.
(3)连接![]() ,
,![]() 交
交![]() 于点
于点![]() ,当
,当![]() ,
,![]() 时,记
时,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,请写出
,请写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义一种新函数:形如![]() (
(![]() ,且
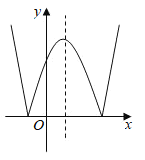
,且![]() )的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2-2x-3|
)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2-2x-3|![]() 的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为
的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为![]() ,
,![]() 和
和![]() ;②图象具有对称性,对称轴是直线
;②图象具有对称性,对称轴是直线![]() ;③当
;③当![]() 或
或![]() 时,函数值
时,函数值![]() 随
随![]() 值的增大而增大;④当
值的增大而增大;④当![]() 或
或![]() 时,函数的最小值是0;⑤当
时,函数的最小值是0;⑤当![]() 时,函数的最大值是4.其中正确结论的个数是______.
时,函数的最大值是4.其中正确结论的个数是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2.下列叙述正确的是( )

A. 小球的飞行高度不能达到15m
B. 小球的飞行高度可以达到25m
C. 小球从飞出到落地要用时4s
D. 小球飞出1s时的飞行高度为10m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com