
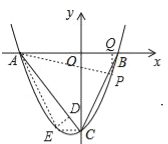
【题目】如图,抛物线y=ax2+bx﹣5(a≠0)与x轴交于点A(﹣5,0)和点B(3,0),与y轴交于点C.
(1)求该抛物线的解析式;
(2)若点E为x轴下方抛物线上的一动点,当S△ABE=S△ABC时,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在点P,使∠BAP=∠CAE?若存在,求出点P的横坐标;若不存在,请说明理由.

【答案】(1)y=![]() x2+
x2+![]() x﹣5;(2)E点坐标为(﹣2,﹣5);(3)存在满足条件的点P,其横坐标为
x﹣5;(2)E点坐标为(﹣2,﹣5);(3)存在满足条件的点P,其横坐标为![]() 或
或![]()
.
【解析】
(1)把A、B两点的坐标代入,利用待定系数法可求得抛物线的解析式;(2)当S△ABE=S△ABC时,可知E点和C点的纵坐标相同,可求得E点坐标;(3)在△CAE中,过E作ED⊥AC于点D,可求得ED和AD的长度,设出点P坐标,过P作PQ⊥x轴于点Q,由条件可知△EDA∽△PQA,利用相似三角形的对应边可得到关于P点坐标的方程,可求得P点坐标.
(1)把A、B两点坐标代入解析式可得![]() ,,解得
,,解得![]() ,
,
∴抛物线解析式为y=![]() x2+
x2+![]() x﹣5;
x﹣5;
(2)在y=![]() x2+
x2+![]() x﹣5中,令x=0可得y=﹣5,
x﹣5中,令x=0可得y=﹣5,
∴C(0,﹣5),
∵S△ABE=S△ABC,且E点在x轴下方,
∴E点纵坐标和C点纵坐标相同,
当y=﹣5时,代入可得![]() x2+
x2+![]() x=﹣5,解得x=﹣2或x=0(舍去),
x=﹣5,解得x=﹣2或x=0(舍去),
∴E点坐标为(﹣2,﹣5);
(3)假设存在满足条件的P点,其坐标为(m,![]() m2+
m2+![]() m﹣5),
m﹣5),
如图,连接AP、CE、AE,过E作ED⊥AC于点D,过P作PQ⊥x轴于点Q,
则AQ=AO+OQ=5+m,PQ=|![]() m2+
m2+![]() m﹣5|,
m﹣5|,
在Rt△AOC中,OA=OC=5,则AC=![]() ,∠ACO=∠DCE=45°,
,∠ACO=∠DCE=45°,
由(2)可得EC=2,在Rt△EDC中,可得DE=DC=![]() ,
,
∴AD=AC﹣DC=![]() ﹣
﹣![]() =4
=4![]() ,
,
当∠BAP=∠CAE时,则△EDA∽△PQA,
∴![]() ,即
,即![]() =
= ,
,
∴![]() m2+
m2+![]() m﹣5=
m﹣5=![]() (5+m)或
(5+m)或![]() m2+
m2+![]() m﹣5=﹣
m﹣5=﹣![]() (5+m),
(5+m),
当![]() m2+
m2+![]() m﹣5=
m﹣5=![]() (5+m)时,整理可得4m2﹣5m﹣75=0,解得m=
(5+m)时,整理可得4m2﹣5m﹣75=0,解得m=![]() 或m=﹣5(与A点重合,舍去),
或m=﹣5(与A点重合,舍去),
当![]() m2+
m2+![]() m﹣5=﹣
m﹣5=﹣![]() (5+m)时,整理可得4m2+11m﹣45=0,解得m=
(5+m)时,整理可得4m2+11m﹣45=0,解得m=![]() 或m=﹣5(与A点重合,舍去),
或m=﹣5(与A点重合,舍去),
∴存在满足条件的点P,其横坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】某商场用14500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表(二)所示:
类别 | 成本价(元/箱) | 销售价(元/箱) |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这500箱矿泉水,可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,边BC在x轴上,点E是对角线AC,BD的交点,反比例函数y=![]() 的图象经过A,E两点,则k的值为( )
的图象经过A,E两点,则k的值为( )
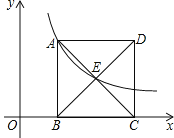
A. 8B. 4C. 6D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
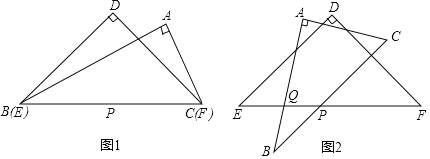
【题目】如图1,含30°和45°角的两块三角板ABC和DEF叠合在一起,边BC与EF重合,BC=EF=12cm,点P为边BC(EF)的中点,现将三角板ABC绕点P按逆时针方向旋转角度α(如图2),设边AB与EF相交于点Q,则当a从0°到90°的变化过程中,点Q移动的路径长为_____(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
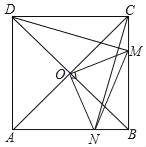
【题目】如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N,连接OM,ON,MN.下列四个结论:①△CNB≌△DMC;②△CON≌△DOM;③△OMN≌△OAD;④AN2+CM2=MN2;其中正确的结论是_____.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
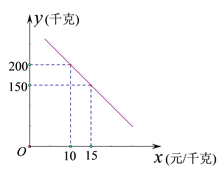
【题目】某乡镇实施产业扶贫,帮助贫困户承包了荒山种植某品种蜜柚.到了收获季节,已知该蜜柚的成本价为8元/千克,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元/千克)之间的函数关系如图所示.
(元/千克)之间的函数关系如图所示.
(1)求![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(2)当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
(3)某农户今年共采摘蜜柚4800千克,该品种蜜柚的保质期为40天,根据(2)中获得最大利润的方式进行销售,能否销售完这批蜜柚?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
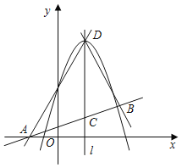
【题目】如图,二次函数![]() 图象的顶点为
图象的顶点为![]() ,对称轴是直线
,对称轴是直线![]() ,一次函数
,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,且与直线
,且与直线![]() 关于
关于![]() 的对称直线交于点
的对称直线交于点![]() .
.
(1)点![]() 的坐标是 ______;
的坐标是 ______;
(2)直线![]() 与直线
与直线![]() 交于点
交于点![]() ,
,![]() 是线段
是线段![]() 上一点(不与点
上一点(不与点![]() 、
、![]() 重合),点
重合),点![]() 的纵坐标为
的纵坐标为![]() .过点
.过点![]() 作直线与线段
作直线与线段![]() 、
、![]() 分别交于点
分别交于点![]() ,
,![]() ,使得
,使得![]() 与
与![]() 相似.
相似.
①当![]() 时,求
时,求![]() 的长;
的长;
②若对于每一个确定的![]() 的值,有且只有一个
的值,有且只有一个![]() 与
与![]() 相似,请直接写出
相似,请直接写出![]() 的取值范围 ______.
的取值范围 ______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】央视热播节目“朗读者”激发了学生的阅读兴趣,某校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:
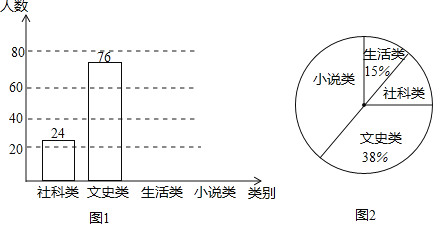
(1)此次共调查了 名学生;
(2)将条形统计图1补充完整;
(3)图2中“小说类”所在扇形的圆心角为 度;
(4)若该校共有学生2000人,估计该校喜欢“社科类”书籍的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,∠CAB=30°,AB=4.5cm.D是线段AB上的一个动点,连接CD,过点D作CD的垂线交CA于点E.设AD=xcm,CE=ycm.(当点D与点A或点B重合时,y的值为5.2)
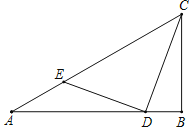
探究函数y随自变量x的变化而变化的规律.
(1)通过取点、画图、测量,得到了x与y的几组对应值,如下表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 |
y/cm | 5.2 | 4.8 | 4.4 | 4.0 | 3.8 | 3.6 | 3.5 | 3.6 | 5.2 |
(要求:补全表格,相关数值保留一位小数)
(2)建立平面直角坐标系xOy,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:当CE=2AD时,AD的长度约为 cm(结果保留一位小数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com