
【题目】如图,二次函数![]() 图象的顶点为
图象的顶点为![]() ,对称轴是直线
,对称轴是直线![]() ,一次函数
,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,且与直线
,且与直线![]() 关于
关于![]() 的对称直线交于点
的对称直线交于点![]() .
.
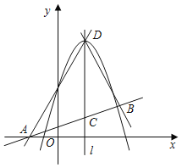
(1)点![]() 的坐标是 ______;
的坐标是 ______;
(2)直线![]() 与直线
与直线![]() 交于点
交于点![]() ,
,![]() 是线段
是线段![]() 上一点(不与点
上一点(不与点![]() 、
、![]() 重合),点
重合),点![]() 的纵坐标为
的纵坐标为![]() .过点
.过点![]() 作直线与线段
作直线与线段![]() 、
、![]() 分别交于点
分别交于点![]() ,
,![]() ,使得
,使得![]() 与
与![]() 相似.
相似.
①当![]() 时,求
时,求![]() 的长;
的长;
②若对于每一个确定的![]() 的值,有且只有一个
的值,有且只有一个![]() 与
与![]() 相似,请直接写出
相似,请直接写出![]() 的取值范围 ______.
的取值范围 ______.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() .
.
【解析】
(1)直接用顶点坐标公式求即可;
(2)由对称轴可知点C(2,![]() ),A(-
),A(-![]() ,0),点A关于对称轴对称的点(
,0),点A关于对称轴对称的点(![]() ,0),借助AD的直线解析式求得B(5,3);①当n=
,0),借助AD的直线解析式求得B(5,3);①当n=![]() 时,N(2,
时,N(2,![]() ),可求DA=
),可求DA=![]() ,DN=
,DN=![]() ,CD=
,CD=![]() ,当PQ∥AB时,△DPQ∽△DAB,DP=9
,当PQ∥AB时,△DPQ∽△DAB,DP=9![]() ;当PQ与AB不平行时,DP=9
;当PQ与AB不平行时,DP=9![]() ;②当PQ∥AB,DB=DP时,DB=3
;②当PQ∥AB,DB=DP时,DB=3![]() ,DN=
,DN=![]() ,所以N(2,
,所以N(2,![]() ),则有且只有一个△DPQ与△DAB相似时,
),则有且只有一个△DPQ与△DAB相似时,![]() <n<
<n<![]() .
.
(1)顶点为![]() ;
;
故答案为![]() ;
;
(2)对称轴![]() ,
,
![]() ,
,
由已知可求![]() ,
,
点![]() 关于
关于![]() 对称点为
对称点为![]() ,
,
则![]() 关于
关于![]() 对称的直线为
对称的直线为![]() ,
,
![]() ,
,
①当![]() 时,
时,![]() ,
,
![]() ,
,![]() ,
,![]()
当![]() 时,
时,![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
当![]() 与
与![]() 不平行时,
不平行时,![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
综上所述![]() ;
;
②当![]() ,
,![]() 时,
时,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴有且只有一个![]() 与
与![]() 相似时,
相似时,![]() ;
;
故答案为![]() ;
;


科目:初中数学 来源: 题型:
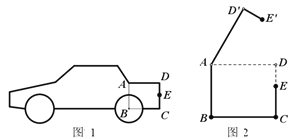
【题目】如图1是某小型汽车的侧面示意图,其中矩形ABCD表示该车的后备箱,在打开后备箱的过程中,箱盖ADE可以绕点A逆时针方向旋转,当旋转角为60°时,箱盖ADE落在AD'E'的位置(如图2所示).已知AD=90厘米,DE=30厘米,EC=40厘米.
(1)求点D'到BC的距离;
(2)求E、E'两点的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)判断以O,A1,B为顶点的三角形的形状.(无须说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣5(a≠0)与x轴交于点A(﹣5,0)和点B(3,0),与y轴交于点C.
(1)求该抛物线的解析式;
(2)若点E为x轴下方抛物线上的一动点,当S△ABE=S△ABC时,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在点P,使∠BAP=∠CAE?若存在,求出点P的横坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 为锐角
为锐角![]() 内部一点,过点
内部一点,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,以
,以![]() 为直径作
为直径作![]() ,交直线
,交直线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() .
.
(2)连接![]() ,当
,当![]() ,
,![]() 时,在点
时,在点![]() 的整个运动过程中.
的整个运动过程中.
①若![]() ,求
,求![]() 的长.
的长.
②若![]() 为等腰三角形,求所有满足条件的
为等腰三角形,求所有满足条件的![]() 的长.
的长.
(3)连接![]() ,
,![]() 交
交![]() 于点
于点![]() ,当
,当![]() ,
,![]() 时,记
时,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,请写出
,请写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
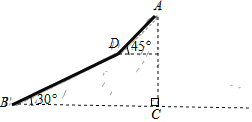
【题目】某地为打造宜游环境,对旅游道路进行改造.如图是风景秀美的观景山,从山脚B到山腰D沿斜坡已建成步行道,为方便游客登顶观景,欲从D到A修建电动扶梯,经测量,山高AC=154米,步行道BD=168米,∠DBC=30°,在D处测得山顶A的仰角为45°.求电动扶梯DA的长(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义一种新函数:形如![]() (
(![]() ,且
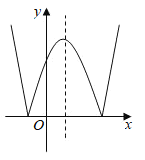
,且![]() )的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2-2x-3|
)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2-2x-3|![]() 的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为
的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为![]() ,
,![]() 和
和![]() ;②图象具有对称性,对称轴是直线
;②图象具有对称性,对称轴是直线![]() ;③当
;③当![]() 或
或![]() 时,函数值
时,函数值![]() 随
随![]() 值的增大而增大;④当
值的增大而增大;④当![]() 或
或![]() 时,函数的最小值是0;⑤当
时,函数的最小值是0;⑤当![]() 时,函数的最大值是4.其中正确结论的个数是______.
时,函数的最大值是4.其中正确结论的个数是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD和正方形AEFG中,边AE在边AB上,AB=![]() ,AE=1.将正方形AEFG绕点A逆时针旋转,设BE的延长线交直线DG于点P,当点P,G第一次重合时停止旋转.在这个过程中:
,AE=1.将正方形AEFG绕点A逆时针旋转,设BE的延长线交直线DG于点P,当点P,G第一次重合时停止旋转.在这个过程中:
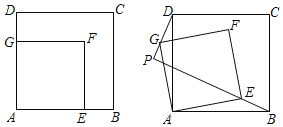
(1)∠BPD=______度;
(2)点P所经过的路径长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台为了解本地区电视节目的收视情况,对部分市民开展了“你最喜爱的电视节目”的问卷调查(每人只填写一项),根据收集的数据绘制了两幅不完整的统计图(如图所示),根据要求回答下列问题:
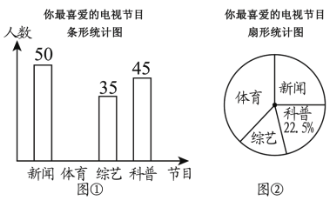
(1)本次问卷调查共调查了________名观众;图②中最喜爱“新闻节目”的人数占调查总人数的百分比为________;
(2)补全图①中的条形统计图;
(3)现有最喜爱“新闻节目”(记为![]() ),“体育节目”(记为
),“体育节目”(记为![]() ),“综艺节目”(记为
),“综艺节目”(记为![]() ),“科普节目”(记为
),“科普节目”(记为![]() )的观众各一名,电视台要从四人中随机抽取两人参加联谊活动,请用列表或画树状图的方法,求出恰好抽到最喜爱“
)的观众各一名,电视台要从四人中随机抽取两人参加联谊活动,请用列表或画树状图的方法,求出恰好抽到最喜爱“![]() ”和“
”和“![]() ”两位观众的概率.
”两位观众的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com