
【题目】如图,已知![]() 为锐角
为锐角![]() 内部一点,过点
内部一点,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,以
,以![]() 为直径作
为直径作![]() ,交直线
,交直线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() .
.
(2)连接![]() ,当
,当![]() ,
,![]() 时,在点
时,在点![]() 的整个运动过程中.
的整个运动过程中.
①若![]() ,求
,求![]() 的长.
的长.
②若![]() 为等腰三角形,求所有满足条件的
为等腰三角形,求所有满足条件的![]() 的长.
的长.
(3)连接![]() ,
,![]() 交
交![]() 于点
于点![]() ,当
,当![]() ,
,![]() 时,记
时,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,请写出
,请写出![]() 的值.
的值.

【答案】(1)见解析;(2)①![]() ;②2,3或
;②2,3或![]() ;(3)见解析;
;(3)见解析;
【解析】
(1)根据垂直的定义得出∠ABP=∠ACP=90°,根据四边形的内角和得出∠BAC+∠BPC=180°,根据平角的定义得出∠BPD+∠BPC=180°,再根据同角的余角相等即可证明结论;
(2)①根据等腰直角三角形的性质得出BP=AB=2![]() ,根据等角的同名三角函数值相等及正切函数的定义得出BP=
,根据等角的同名三角函数值相等及正切函数的定义得出BP=![]() PD,从而得出PD的长;
PD,从而得出PD的长;
②当BD=BE时,∠BED=∠BDE,故∠BPD=∠BPE=∠BAC,根据等角的同名三角函数值相等得出tan∠BPE=2,根据正切函数的定义,由AB=2![]() 得出BP=
得出BP=![]() ,根据勾股定理即可求出BD;
,根据勾股定理即可求出BD;
当BE=DE时,∠EBD=∠EDB,由∠APB=∠BDE,∠DBE=∠APC,得出∠APB=∠APC,则AC=AB=2![]() ,过点B作BG⊥AC于点G,得四边BGCD是矩形,根据正切函数的定义得出AG=2,进而可求出BD;
,过点B作BG⊥AC于点G,得四边BGCD是矩形,根据正切函数的定义得出AG=2,进而可求出BD;
当BD=DE时,∠DEB=∠DBE=∠APC,由∠DEB=∠DPB=∠BAC得出∠APC=∠BAC,设PD=x,则BD=2x,根据正切函数的定义列出关于x的方程,求解得出x的值,进而由BD=2x得出答案;
(3),过点O作OH上DC于点H,根据tan∠BPD=tan∠MAN=1得出BD=DP,令BD=DP=2a,PC=2b得OH=a,CH=a+2b.AC=4a+2b,证△ACP∽△CHO得![]() ,据此得出a=b及CP=2a、CH=3a、OC=
,据此得出a=b及CP=2a、CH=3a、OC=![]() a,再根据△CPF∽△COH,
a,再根据△CPF∽△COH,
得![]() ,据此求得CF=
,据此求得CF=![]() ,OF=
,OF=![]() ,证OF为△PBE的中位线知EF=PF,从而依据
,证OF为△PBE的中位线知EF=PF,从而依据![]() 可得答案.
可得答案.
(1)解:
∵![]() ,
,![]()
∴![]()
∴![]()
∵![]()
∴![]()
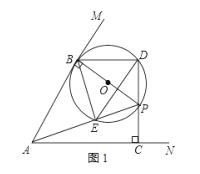
(2)解:①如图1,
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
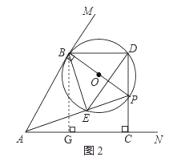
②如图2,当![]() 时,∴
时,∴![]()
∴![]()
∵![]() ,∴
,∴![]()
在![]() 中,
中,![]() ,设
,设![]() ,则
,则![]() ,∴
,∴![]() ,解得
,解得![]()
∴![]()
当![]() 时,
时,![]()
∵![]()
∴![]()
∴![]()
过点![]() 作
作![]() 于点
于点![]() ,得四边形
,得四边形![]() 是矩形
是矩形
∵![]() ,
,![]()
∴![]()
∴![]()
当![]() 时,
时,![]()
∵![]()
∴![]()
设![]() ,则
,则![]()
∴![]() ,∴
,∴![]()
∴![]() ,∴
,∴![]()
综上所述,当![]() 为2,3或
为2,3或![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.
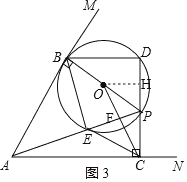
(3)如图3,过点O作OH⊥DC于点H,
∵tan∠BPD=tan∠MAN=1,
∴BD=PD,
设BD=PD=2a、PC=2b,
则OH=a、CH=a+2b、AC=4a+2b,
∵OC∥BE且∠BEP=90°,
∴∠PFC=90°,
∴∠PAC+∠APC=∠OCH+∠APC=90°,
∴∠OCH=∠PAC,
∴△ACP∽△CHO,
∴![]() ,即OHAC=CHPC,
,即OHAC=CHPC,
∴a(4a+2b)=2b(a+2b),
∴a=b,
即CP=2a、CH=3a,
则OC=![]() a,
a,
∵△CPF∽△COH,
∴![]() ,即
,即![]() ,
,
则CF=![]() ,OF=OCCF=
,OF=OCCF=![]() ,
,
∵BE∥OC且BO=PO,
∴OF为△PBE的中位线,
∴EF=PF,
∴![]()


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点D在⊙O的直径AB延长线上,点C在⊙O上,过点D作ED⊥AD,与AC的延长线相交于点E,且CD=DE.
(1)求证:CD为⊙O的切线;
(2)若AB=12,且BC=CE时,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1:![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)

(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() 1.414,
1.414,![]() 1.732)
1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
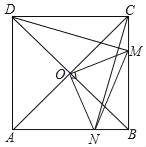
【题目】如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N,连接OM,ON,MN.下列四个结论:①△CNB≌△DMC;②△CON≌△DOM;③△OMN≌△OAD;④AN2+CM2=MN2;其中正确的结论是_____.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的对称轴为直线x=﹣1,部分图象如图所示,下列判断中:
①abc>0;
②b2﹣4ac>0;
③9a﹣3b+c=0;
④若点(﹣0.5,y1),(﹣2,y2)均在抛物线上,则y1>y2;
⑤5a﹣2b+c<0.
其中正确的个数有( )
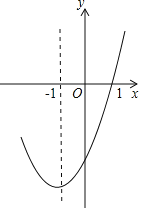
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 图象的顶点为
图象的顶点为![]() ,对称轴是直线
,对称轴是直线![]() ,一次函数
,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,且与直线
,且与直线![]() 关于
关于![]() 的对称直线交于点
的对称直线交于点![]() .
.
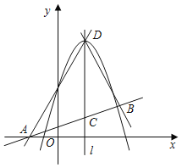
(1)点![]() 的坐标是 ______;
的坐标是 ______;
(2)直线![]() 与直线
与直线![]() 交于点
交于点![]() ,
,![]() 是线段
是线段![]() 上一点(不与点
上一点(不与点![]() 、
、![]() 重合),点
重合),点![]() 的纵坐标为
的纵坐标为![]() .过点
.过点![]() 作直线与线段
作直线与线段![]() 、
、![]() 分别交于点
分别交于点![]() ,
,![]() ,使得
,使得![]() 与
与![]() 相似.
相似.
①当![]() 时,求
时,求![]() 的长;
的长;
②若对于每一个确定的![]() 的值,有且只有一个
的值,有且只有一个![]() 与
与![]() 相似,请直接写出
相似,请直接写出![]() 的取值范围 ______.
的取值范围 ______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划组织240名师生到红色教育基地开展革命传统教育活动.旅游公司有A,B两种客车可供租用,A型客车每辆载客量45人,B型客车每辆载客量30人.若租用4辆A型客车和3辆B型客车共需费用10700元;若租用3辆A型客车和4辆B型客车共需费用10300元.
(1)求租用A,B两型客车,每辆费用分别是多少元;
(2)为使240名师生有车坐,且租车总费用不超过1万元,你有哪几种租车方案?哪种方案最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=6,将△ABC绕点B逆时针旋转60°得到△A'BC’,连接A'C,则A'C的长为( )
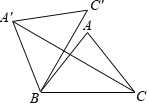
A. 6B. 4+2![]() C. 4+3
C. 4+3![]() D. 2+3
D. 2+3![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com