
【题目】如图,正方形ABCD的边长为4,边BC在x轴上,点E是对角线AC,BD的交点,反比例函数y=![]() 的图象经过A,E两点,则k的值为( )
的图象经过A,E两点,则k的值为( )
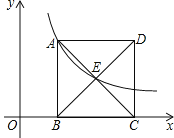
A. 8B. 4C. 6D. 3
科目:初中数学 来源: 题型:
【题目】某菜市场有2.5平方米和4平方米两种摊位,2.5平方米的摊位数是4平方米摊位数的2倍.管理单位每月底按每平方米20元收取当月管理费,该菜市场全部摊位都有商户经营且各摊位均按时全额缴纳管理费.
(1)菜市场毎月可收取管理费4500元,求该菜市场共有多少个4平方米的摊位?
(2)为推进环保袋的使用,管理单位在5月份推出活动一:“使用环保袋送礼物”,2.5平方米和4平方米两种摊位的商户分别有40%和20%参加了此项活动.为提高大家使用环保袋的积极性,6月份准备把活动一升级为活动二:“使用环保袋抵扣管理费”,同时终止活动一.经调査与测算,参加活动一的商户会全部参加活动二,参加活动二的商户会显著增加,这样,6月份参加活动二的2.5平方米摊位的总个数将在5月份参加活动一的同面积个数的基础上增加2a%,毎个摊位的管理费将会减少![]() ;6月份参加活动二的4平方米摊位的总个数将在5月份参加活动一的同面积个数的基础上增加6a%,每个摊位的管理费将会减少
;6月份参加活动二的4平方米摊位的总个数将在5月份参加活动一的同面积个数的基础上增加6a%,每个摊位的管理费将会减少![]() .这样,参加活动二的这部分商户6月份总共缴纳的管理费比他们按原方式共缴纳的管理费将减少
.这样,参加活动二的这部分商户6月份总共缴纳的管理费比他们按原方式共缴纳的管理费将减少![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是某小型汽车的侧面示意图,其中矩形ABCD表示该车的后备箱,在打开后备箱的过程中,箱盖ADE可以绕点A逆时针方向旋转,当旋转角为60°时,箱盖ADE落在AD'E'的位置(如图2所示).已知AD=90厘米,DE=30厘米,EC=40厘米.
(1)求点D'到BC的距离;
(2)求E、E'两点的距离.
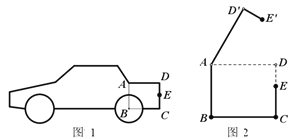
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
第一步,分别以点A、D为圆心,以大于![]() AD的长为半径在AD两侧作弧,交于两点M、N;
AD的长为半径在AD两侧作弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF.
若BD=6,AF=4,CD=3,求线段BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
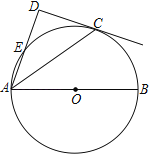
【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
(1)求证:AC平分∠DAB;
(2)连接BC,若cos∠CAD=![]() ,⊙O的半径为5,求CD、AE的值.
,⊙O的半径为5,求CD、AE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)判断以O,A1,B为顶点的三角形的形状.(无须说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣5(a≠0)与x轴交于点A(﹣5,0)和点B(3,0),与y轴交于点C.
(1)求该抛物线的解析式;
(2)若点E为x轴下方抛物线上的一动点,当S△ABE=S△ABC时,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在点P,使∠BAP=∠CAE?若存在,求出点P的横坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD和正方形AEFG中,边AE在边AB上,AB=![]() ,AE=1.将正方形AEFG绕点A逆时针旋转,设BE的延长线交直线DG于点P,当点P,G第一次重合时停止旋转.在这个过程中:
,AE=1.将正方形AEFG绕点A逆时针旋转,设BE的延长线交直线DG于点P,当点P,G第一次重合时停止旋转.在这个过程中:
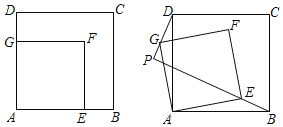
(1)∠BPD=______度;
(2)点P所经过的路径长为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com