
【题目】ABCD中,E、F分别在边AB和CD上,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】B
【解析】
根据平行四边形的判定方法对各个选项进行分析判断即可.
解:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,AD=BC,AD∥BC,∠B=∠D;

A.AE=CF时,由AE∥CF,AE=CF,可以得出四边形AECF是平行四边形;
B.AF=EC时,不能得出四边形AECF一定为平行四边形;
C.∠DAF=∠BCE时,可以得出△ADF≌△CBE,得出AF=CE,DF=BE,因此AE=CF,可以证出四边形AECF是平行四边形;
D.∠AFD=∠CEB时,可以得出△ADF≌△CBE,得出AF=CE,DF=BE,因此AE=CF,可以证出四边形AECF是平行四边形;
故选:B.


 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中有1个白球3个红球,每个小球除颜色外其他都相同.
(1)搅匀后,甲先从袋中随机取出1个小球,记下颜色后不放回;乙再从袋中随机取出1个小球.用画树状图或列表的方法,求甲乙两人取出的都是红球的概率;
(2)搅匀后从中任意取出一个球,要使取出红球的概率为![]() ,应添加几个什么颜色的球?
,应添加几个什么颜色的球?
查看答案和解析>>
科目:初中数学 来源: 题型:
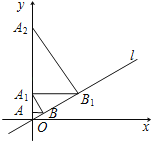
【题目】如图,已知直线l:![]() ,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;……按此作法继续下去,则点A2019的坐标为_____.
,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;……按此作法继续下去,则点A2019的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,边BC在x轴上,点E是对角线AC,BD的交点,反比例函数y=![]() 的图象经过A,E两点,则k的值为( )
的图象经过A,E两点,则k的值为( )
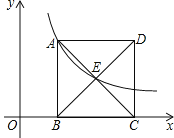
A. 8B. 4C. 6D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场里某产品每月销售量y(只)与销售单价x(元)满足一次函数关系,经调查部分数据如表:(已知每只进价为10元,每只利润=销售单价-进价)
销售单价x(元) | 21 | 23 | 25 | … |
月销售额y(只) | 29 | 27 | 25 | … |
(1)求出y与x之间的函数表达式;
(2)这产品每月的总利润为w元,求w关于x的函数表达式,并指出销售单价为多少元时利润最大,最大利润是多少元?
(3)由于该产品市场需求量较大,进价在原有基础上提高了a元(a<10),但每月销售量与销售价仍满足上述一次函数关系,此时,随着销售量的增大,所得的最大利润比(2)中的最大利润减少了144元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
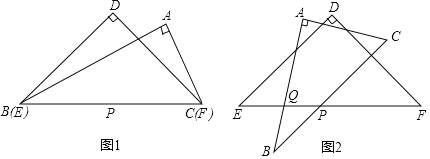
【题目】如图1,含30°和45°角的两块三角板ABC和DEF叠合在一起,边BC与EF重合,BC=EF=12cm,点P为边BC(EF)的中点,现将三角板ABC绕点P按逆时针方向旋转角度α(如图2),设边AB与EF相交于点Q,则当a从0°到90°的变化过程中,点Q移动的路径长为_____(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
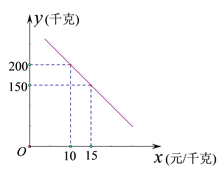
【题目】某乡镇实施产业扶贫,帮助贫困户承包了荒山种植某品种蜜柚.到了收获季节,已知该蜜柚的成本价为8元/千克,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元/千克)之间的函数关系如图所示.
(元/千克)之间的函数关系如图所示.
(1)求![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(2)当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
(3)某农户今年共采摘蜜柚4800千克,该品种蜜柚的保质期为40天,根据(2)中获得最大利润的方式进行销售,能否销售完这批蜜柚?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
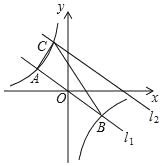
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
(1)求反比例函数的表达式;
(2)将直线l1:y=﹣![]() x向上平移后的直线l2与反比例函数y=
x向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com