
ЁОЬтФПЁПЩЬГЁРяФГВњЦЗУПдТЯњЪлСПyЃЈжЛЃЉгыЯњЪлЕЅМлxЃЈдЊЃЉТњзувЛДЮКЏЪ§ЙиЯЕЃЌОЕїВщВПЗжЪ§ОнШчБэЃКЃЈвбжЊУПжЛНјМлЮЊ10дЊЃЌУПжЛРћШѓ=ЯњЪлЕЅМл-НјМлЃЉ
ЯњЪлЕЅМлxЃЈдЊЃЉ | 21 | 23 | 25 | Ё |
дТЯњЪлЖюyЃЈжЛЃЉ | 29 | 27 | 25 | Ё |
ЃЈ1ЃЉЧѓГіyгыxжЎМфЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉетВњЦЗУПдТЕФзмРћШѓЮЊwдЊЃЌЧѓwЙигкxЕФКЏЪ§БэДяЪНЃЌВЂжИГіЯњЪлЕЅМлЮЊЖрЩйдЊЪБРћШѓзюДѓЃЌзюДѓРћШѓЪЧЖрЩйдЊЃП
ЃЈ3ЃЉгЩгкИУВњЦЗЪаГЁашЧѓСПНЯДѓЃЌНјМлдкдгаЛљДЁЩЯЬсИпСЫaдЊЃЈaЃМ10ЃЉЃЌЕЋУПдТЯњЪлСПгыЯњЪлМлШдТњзуЩЯЪівЛДЮКЏЪ§ЙиЯЕЃЌДЫЪБЃЌЫцзХЯњЪлСПЕФдіДѓЃЌЫљЕУЕФзюДѓРћШѓБШЃЈ2ЃЉжаЕФзюДѓРћШѓМѕЩйСЫ144дЊЃЌЧѓaЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=-x+50ЃЛЃЈ2ЃЉЕБЯњЪлЕЅМлЖЈЮЊ30дЊЪБЃЌУПдТПЩЛёЕУзюДѓРћШѓ400дЊЃЛЃЈ3ЃЉ8ЃЛ
ЁОНтЮіЁП
![]() Д§ЖЈЯЕЪ§ЗЈЧѓКЏЪ§НтЮіЪНЃЎ
Д§ЖЈЯЕЪ§ЗЈЧѓКЏЪ§НтЮіЪНЃЎ
![]() змРћШѓ
змРћШѓ![]() ЕЅМўРћШѓ
ЕЅМўРћШѓ![]() змЯњЪлСПЃЌЯШБэЪОГіwЃЌдйИљОнЖўДЮКЏЪ§ЧѓзюжЕЮЪЬтНјааХфЗНМДПЩЃЎ
змЯњЪлСПЃЌЯШБэЪОГіwЃЌдйИљОнЖўДЮКЏЪ§ЧѓзюжЕЮЪЬтНјааХфЗНМДПЩЃЎ
![]() КЌВЮЕФЖўДЮКЏЪ§ЮЪЬтЃЌЯШБэЪОГіwЃЌИљОнзюДѓРћШѓСаЗНГЬМДПЩЧѓГіaЃЎ
КЌВЮЕФЖўДЮКЏЪ§ЮЪЬтЃЌЯШБэЪОГіwЃЌИљОнзюДѓРћШѓСаЗНГЬМДПЩЧѓГіaЃЎ
НтЃКЃЈ1ЃЉЩшy=kx+bЃЈkЁй0ЃЉЃЌ
ИљОнЬтвтДњШыЕуЃЈ21ЃЌ29ЃЉЃЌЃЈ25ЃЌ25ЃЉЃЌ
Ёр![]()
НтЕУ![]() ЃЌ
ЃЌ
Ёрy=-x+50ЃЎ
ЃЈ2ЃЉвРЬтвтЕУЃЌw=ЃЈx-10ЃЉЃЈ-x+50ЃЉ=-x2+60x-500=-ЃЈx-30ЃЉ2+400ЃЌ
Ёпa=-1ЃМ0ЃЌ
ЁрЕБx=30ЪБЃЌwгазюДѓжЕ400ЃЌ
МДЕБЯњЪлЕЅМлЖЈЮЊ30дЊЪБЃЌУПдТПЩЛёЕУзюДѓРћШѓ400дЊЃЎ
ЃЈ3ЃЉзюаТРћШѓПЩБэЪОЮЊ-x2+60x-500-aЃЈ-x+50ЃЉ=-x2+ЃЈ60+aЃЉx-500-50aЃЌ
ЁрДЫЪБзюДѓРћШѓЮЊ![]() =400-144ЃЌ
=400-144ЃЌ
НтЕУa1=8ЃЌa2=72ЃЌ
ЁпЕБa=72ЪБЃЌЯњСПЮЊИКЪ§ЩсШЅЃЎ
Ёрa=8ЃЎ


 жЧШЄКЎМйзївЕдЦФЯПЦММГіАцЩчЯЕСаД№АИ
жЧШЄКЎМйзївЕдЦФЯПЦММГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() ОЕу
ОЕу![]() ЃЌгы
ЃЌгы![]() жсЯрНЛгкЕу
жсЯрНЛгкЕу![]() ЃЎ
ЃЎ
(1)ЧѓХзЮяЯпЕФНтЮіЪНЃЛ
(2)ЖЈвхЃКЦНУцЩЯЕФШЮвЛЕуЕНЖўДЮКЏЪ§ЭМЯѓЩЯгыЫќКсзјБъЯрЭЌЕФЕуЕФОрРыЃЌГЦЮЊЕуЕНЖўДЮКЏЪ§ЭМЯѓЕФДЙжБОрРыЃЎШчЃКЕу![]() ЕНЖўДЮКЏЪ§ЭМЯѓЕФДЙжБОрРыЪЧЯпЖЮ
ЕНЖўДЮКЏЪ§ЭМЯѓЕФДЙжБОрРыЪЧЯпЖЮ![]() ЕФГЄЃЎвбжЊЕу
ЕФГЄЃЎвбжЊЕу![]() ЮЊХзЮяЯпЖдГЦжсЩЯЕФвЛЕуЃЌЧвдк
ЮЊХзЮяЯпЖдГЦжсЩЯЕФвЛЕуЃЌЧвдк![]() жсЩЯЗНЃЌЕу
жсЩЯЗНЃЌЕу![]() ЮЊЦНУцФквЛЕуЃЌЕБвд
ЮЊЦНУцФквЛЕуЃЌЕБвд![]() ЮЊЖЅЕуЕФЫФБпаЮЪЧБпГЄЮЊ4ЕФСтаЮЪБЃЌЧыЧѓГіЕу
ЮЊЖЅЕуЕФЫФБпаЮЪЧБпГЄЮЊ4ЕФСтаЮЪБЃЌЧыЧѓГіЕу![]() ЕНЖўДЮКЏЪ§ЭМЯѓЕФДЙжБОрРыЃЎ
ЕНЖўДЮКЏЪ§ЭМЯѓЕФДЙжБОрРыЃЎ
(3)дк(2)жаЃЌЕБЕу![]() ЕНЖўДЮКЏЪ§ЭМЯѓЕФДЙжБОрРызюаЁЪБЃЌдк
ЕНЖўДЮКЏЪ§ЭМЯѓЕФДЙжБОрРызюаЁЪБЃЌдк![]() ЮЊЖЅЕуЕФСтаЮФкВПЪЧЗёДцдкЕу
ЮЊЖЅЕуЕФСтаЮФкВПЪЧЗёДцдкЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() жЎКЭзюаЁЃЌШєДцдкЃЌЧыЧѓГізюаЁжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
жЎКЭзюаЁЃЌШєДцдкЃЌЧыЧѓГізюаЁжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
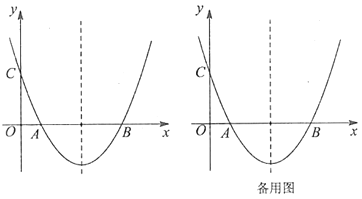
ЁОЬтФПЁПШчЭМ1ЃЌдкжБНЧЁїABCжаЃЌЁЯACB=90ЁуЃЌAOЪЧЁїABCЕФНЧЦНЗжЯпЃЌвдOЮЊдВаФЃЌOCЮЊАыОЖзїдВO
ЃЈ1ЃЉЧѓжЄЃКABЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉвбжЊAOНЛдВOгкЕуEЃЌбгГЄAOНЛдВOгкЕуDЃЌtanЁЯD=![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌдкЃЈ2ЃЉЬѕМўЯТЃЌШєABгыЁбOЕФЧаЕуЮЊЕуFЃЌСЌНгCFНЛADгкЕуGЃЌЩшЁбOЕФАыОЖЮЊ3ЃЌЧѓCFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
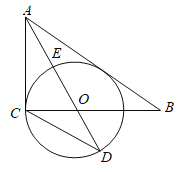
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпyЃНx2+bx+cгыxжсНЛгкЕуAЃЌBЃЌABЃН2ЃЌгыyжсНЛгкЕуCЃЌЖдГЦжсЮЊжБЯпxЃН2ЃЎ
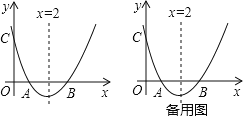
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЩшDЮЊХзЮяЯпЕФЖЅЕуЃЌСЌНгDAЁЂDBЃЌЪдХаЖЯЁїABDЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЩшPЮЊЖдГЦжсЩЯвЛЖЏЕуЃЌвЊЪЙPCЉPBЕФжЕзюДѓЃЌЧѓГіPЕуЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПABCDжаЃЌEЁЂFЗжБ№дкБпABКЭCDЩЯЃЌЯТСаЬѕМўжаЃЌВЛФмЕУГіЫФБпаЮAECFвЛЖЈЮЊЦНааЫФБпаЮЕФЪЧЃЈЁЁЁЁЃЉ
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЗДБШР§КЏЪ§yЃН![]() ЃЈxЃМ0ЃЉЕФЭМЯѓОЙ§OABCЕФЖЅЕуBЃЌЕуAдкxжсЩЯЃЌACЁЭxжсНЛЗДБШР§КЏЪ§ЭМЯѓгкЕуDЃЌBEЁЭxжсгкЕуEЃЌдђBEЃКADЃНЃЈЁЁЁЁЃЉ
ЃЈxЃМ0ЃЉЕФЭМЯѓОЙ§OABCЕФЖЅЕуBЃЌЕуAдкxжсЩЯЃЌACЁЭxжсНЛЗДБШР§КЏЪ§ЭМЯѓгкЕуDЃЌBEЁЭxжсгкЕуEЃЌдђBEЃКADЃНЃЈЁЁЁЁЃЉ
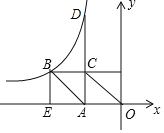
A. 1ЃК2B. 1ЃК![]() C. 1ЃК3D. 1ЃК
C. 1ЃК3D. 1ЃК![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПРрБШЕШбќШ§НЧаЮЕФЖЈвхЃЌЮвУЧЖЈвхЃКгаШ§ЬѕБпЯрЕШЕФЭЙЫФБпаЮНазіЁАзМЕШБпЫФБпаЮЁБ
ЃЈ1ЃЉвбжЊЃКШчЭМ1ЃЌдкЁАзМЕШБпЫФБпаЮЁБABCDжаЃЌBCЁйABЃЌBDЁЭCDЃЌABЃН3ЃЌBDЃН4ЃЌЧѓBCЕФГЄЃЛ
ЃЈ2ЃЉдкЬНОПаджЪЪБЃЌаЁУїЗЂЯжвЛИіНсТлЃКЖдНЧЯпЛЅЯрДЙжБЕФЁАзМЕШБпЫФБпаЮЁБЪЧСтаЮЃЎЧыФуХаЖЯДЫНсТлЪЧЗёе§ШЗЃЌШєе§ШЗЃЌЧыЫЕУїРэгЩЃЛШєВЛе§ШЗЃЌЧыОйГіЗДР§ЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌдкЁїABCжаЃЌABЃНACЃЌЁЯBACЃН90ЁуЃЌBCЃН2ЃЎдкABЕФДЙжБЦНЗжЯпЩЯЪЧЗёДцдкЕуPЪЙЕУвдAЃЌBЃЌCЃЌPЮЊЖЅЕуЕФЫФБпаЮЮЊЁАзМЕШБпЫФБпаЮЁБЃПШєДцдкЃЌЧыЧѓГіИУЁАзМЕШБпЫФБпаЮЁБЕФУцЛ§ЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПГТРЯЪІЖдЫћЫљНЬЕФОХЃЈ1ЃЉЁЂОХЃЈ2ЃЉСНИіАрМЖЕФбЇЩњНјааСЫвЛДЮМьВтЃЌХњдФКѓЖдзюКѓвЛЕРЪдЬтЕФЕУЗжЧщПіНјааСЫЙщРрЭГМЦЃЈИїРрБ№ЕФЕУЗжШчЯТБэЃЉЃЌВЂЛцжЦСЫШчЭМЫљЪОЕФУПАрИїРрБ№ЕУЗжШЫЪ§ЕФЬѕаЮЭГМЦЭМЃЈВЛЭъећЃЉЃЎ
ИїРрБ№ЕФЕУЗжБэ
ЕУЗж | РрБ№ |
|
|
|
|
|
|
|
|
вбжЊСНИіАрвЛЙВга![]() ЕФбЇЩњЕУЕНСНИіе§ШЗД№АИЃЌНтД№ЭъШЋе§ШЗЃЌОХЃЈ1ЃЉАрбЇЩњетЕРЪдЬтЕФЦНОљЕУЗжЮЊ
ЕФбЇЩњЕУЕНСНИіе§ШЗД№АИЃЌНтД№ЭъШЋе§ШЗЃЌОХЃЈ1ЃЉАрбЇЩњетЕРЪдЬтЕФЦНОљЕУЗжЮЊ![]() ЗжЃЎЧыНтОіШчЯТЮЪЬтЃК
ЗжЃЎЧыНтОіШчЯТЮЪЬтЃК
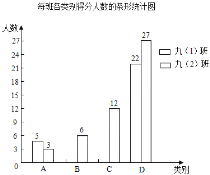
ЃЈ1ЃЉОХЃЈ2ЃЉАрбЇЩњЕУЗжЕФжаЮЛЪ§ЪЧ ______ЃЛ
ЃЈ2ЃЉОХЃЈ1ЃЉАрбЇЩњжаетЕРЪдЬтзїД№ЧщПіЪєгк![]() РрКЭ
РрКЭ![]() РрЕФШЫЪ§ИїЪЧЖрЩйЃП
РрЕФШЫЪ§ИїЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
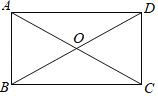
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮABCDжаЃЌACЁЂBDЯрНЛгкЕуOЃЌЧвAOЃНCOЃЌABЁЮCDЃЎ
ЃЈ1ЃЉЧѓжЄЃКABЃНCDЃЛ
ЃЈ2ЃЉШєЁЯOABЃНЁЯOBAЃЌЧѓжЄЃКЫФБпаЮABCDЪЧОиаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com