
【题目】如图,已知反比例函数y=![]() (x<0)的图象经过OABC的顶点B,点A在x轴上,AC⊥x轴交反比例函数图象于点D,BE⊥x轴于点E,则BE:AD=( )
(x<0)的图象经过OABC的顶点B,点A在x轴上,AC⊥x轴交反比例函数图象于点D,BE⊥x轴于点E,则BE:AD=( )
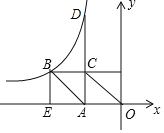
A. 1:2B. 1:![]() C. 1:3D. 1:
C. 1:3D. 1:![]()
科目:初中数学 来源: 题型:
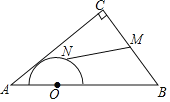
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最小值和最大值之和是( )
,点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最小值和最大值之和是( )
A. 5B. 6C. 7D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E,F,则图中阴影部分的面积为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
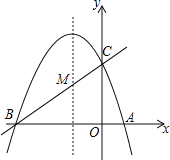
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场里某产品每月销售量y(只)与销售单价x(元)满足一次函数关系,经调查部分数据如表:(已知每只进价为10元,每只利润=销售单价-进价)
销售单价x(元) | 21 | 23 | 25 | … |
月销售额y(只) | 29 | 27 | 25 | … |
(1)求出y与x之间的函数表达式;
(2)这产品每月的总利润为w元,求w关于x的函数表达式,并指出销售单价为多少元时利润最大,最大利润是多少元?
(3)由于该产品市场需求量较大,进价在原有基础上提高了a元(a<10),但每月销售量与销售价仍满足上述一次函数关系,此时,随着销售量的增大,所得的最大利润比(2)中的最大利润减少了144元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,10×10的网格中,A,B,C均在格点上,诮用无刻度的直尺作直线MN,使得直线MN平分△ABC的周长(留作图痕迹,不写作法)
(1)请在图1中作出符合要求的一条直线MN;
(2)如图2,点M为BC上一点,BM=5.请在AB上作出点N的位置.

查看答案和解析>>
科目:初中数学 来源: 题型:
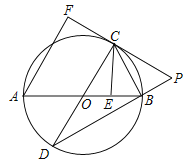
【题目】(2017广东省)如图,AB是⊙O的直径,AB=![]() ,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.
,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.
(1)求证:CB是∠ECP的平分线;
(2)求证:CF=CE;
(3)当![]() 时,求劣弧
时,求劣弧![]() 的长度(结果保留π)
的长度(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
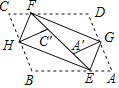
【题目】如图,平行四边形纸片ABCD的边AB,BC的长分别是10cm和7.5cm,将其四个角向内对折后,点B与点C重合于点C',点A与点D重合于点A′.四条折痕围成一个“信封四边形”EHFG,其顶点分别在平行四边形ABCD的四条边上,则EF=__cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
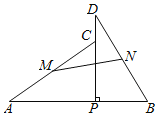
【题目】如图,线段AB=1,点P是线段AB上一个动点(不包括A、B)在AB同侧作Rt△PAC,Rt△PBD,∠A=∠D=30°,∠APC=∠BPD=90°,M、N分别是AC、BD的中点,连接MN,设AP=x,MN2=y,则y关于x的函数图象为( )
A. 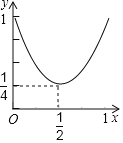 B.
B. 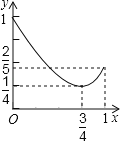
C. 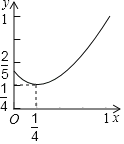 D.
D. 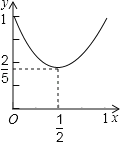
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com