
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最小值和最大值之和是( )
,点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最小值和最大值之和是( )
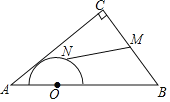
A. 5B. 6C. 7D. 8
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xoy中(如图),已知一次函数的图像平行于直线![]() ,且经过点A(2,3),与x轴交于点B。
,且经过点A(2,3),与x轴交于点B。
(1)求这个一次函数的解析式;
(2)设点C在y轴上,当AC=BC时,求点C的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
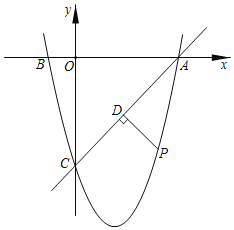
【题目】如图,在平面直角坐标系中,已知点![]() 的坐标为
的坐标为![]() ,且
,且![]() ,抛物线
,抛物线![]() 图象经过
图象经过![]() 三点.
三点.
(1)求![]() 两点的坐标;
两点的坐标;
(2)求抛物线的解析式;
(3)若点![]() 是直线
是直线![]() 下方的抛物线上的一个动点,作
下方的抛物线上的一个动点,作![]() 于点
于点![]() ,当
,当![]() 的值最大时,求此时点
的值最大时,求此时点![]() 的坐标及
的坐标及![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
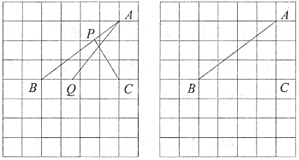
【题目】如图,在由边长都为1的小正方形组成的网格中,点![]() ,
,![]() ,
,![]() 均为格点,点
均为格点,点![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 上的动点,且满足
上的动点,且满足![]() .
.
(1)线段![]() 的长度等于__________;
的长度等于__________;
(2)当线段![]() 取得最小值时,请借助无刻度直尺在给定的网格中画出线段
取得最小值时,请借助无刻度直尺在给定的网格中画出线段![]() 和
和![]() ,并简要说明你是怎么画出点Q,P的:_______________________.
,并简要说明你是怎么画出点Q,P的:_______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经点
经点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
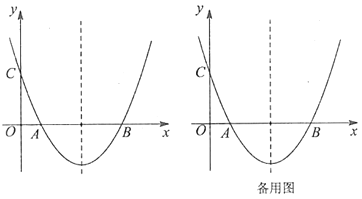
(1)求抛物线的解析式;
(2)定义:平面上的任一点到二次函数图象上与它横坐标相同的点的距离,称为点到二次函数图象的垂直距离.如:点![]() 到二次函数图象的垂直距离是线段
到二次函数图象的垂直距离是线段![]() 的长.已知点
的长.已知点![]() 为抛物线对称轴上的一点,且在
为抛物线对称轴上的一点,且在![]() 轴上方,点
轴上方,点![]() 为平面内一点,当以
为平面内一点,当以![]() 为顶点的四边形是边长为4的菱形时,请求出点
为顶点的四边形是边长为4的菱形时,请求出点![]() 到二次函数图象的垂直距离.
到二次函数图象的垂直距离.
(3)在(2)中,当点![]() 到二次函数图象的垂直距离最小时,在
到二次函数图象的垂直距离最小时,在![]() 为顶点的菱形内部是否存在点
为顶点的菱形内部是否存在点![]() ,使得
,使得![]() 之和最小,若存在,请求出最小值;若不存在,请说明理由.
之和最小,若存在,请求出最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
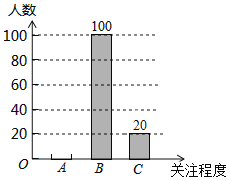
【题目】湖南省作为全国第三批启动高考综合改革的省市之一,从2018年秋季入学的高中一年级学生开始实施高考综合改革.深化高考综合改革,承载着广大考生的美好期盼,事关千家万户的切身利益,社会关注度高.为了了解我市某小区居民对此政策的关注程度,某数学兴趣小组随机采访了该小区部分居民,根据采访情况制做了如统计图表:
关注程度 | 频数 | 频率 |
A.高度关注 | m | 0.4 |
B.一般关注 | 100 | 0.5 |
C.没有关注 | 20 | n |
(1)根据上述统计图表,可得此次采访的人数为 ,m= ,n= .
(2)根据以上信息补全图中的条形统计图.
(3)请估计在该小区1500名居民中,高度关注新高考政策的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
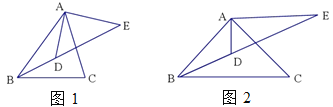
【题目】如图1,AD、BD分别是△ABC的内角∠BAC、∠ABC的平分线,过点A作AE上AD,交BD的延长线于点E.
(1)求证:∠E=![]() ∠C;
∠C;
(2)如图2,如果AE=AB,且BD:DE=2:3,求cos∠ABC的值;
(3)如果∠ABC是锐角,且△ABC与△ADE相似,求∠ABC的度数,并直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=![]() (x<0)的图象经过OABC的顶点B,点A在x轴上,AC⊥x轴交反比例函数图象于点D,BE⊥x轴于点E,则BE:AD=( )
(x<0)的图象经过OABC的顶点B,点A在x轴上,AC⊥x轴交反比例函数图象于点D,BE⊥x轴于点E,则BE:AD=( )
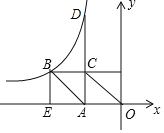
A. 1:2B. 1:![]() C. 1:3D. 1:
C. 1:3D. 1:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com