
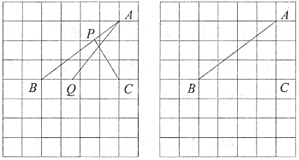
【题目】如图,在由边长都为1的小正方形组成的网格中,点![]() ,
,![]() ,
,![]() 均为格点,点
均为格点,点![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 上的动点,且满足
上的动点,且满足![]() .
.
(1)线段![]() 的长度等于__________;
的长度等于__________;
(2)当线段![]() 取得最小值时,请借助无刻度直尺在给定的网格中画出线段
取得最小值时,请借助无刻度直尺在给定的网格中画出线段![]() 和
和![]() ,并简要说明你是怎么画出点Q,P的:_______________________.
,并简要说明你是怎么画出点Q,P的:_______________________.
【答案】5 取格点![]() .连接
.连接![]() ,它们相交于点
,它们相交于点![]() ,连接
,连接![]() ,分别交
,分别交![]() 于点
于点![]() ,则线段
,则线段![]() 和
和![]() 即为所求.
即为所求.
【解析】
(1)利用勾股定理求出AB的长即可;(2)要使AQ+PC有最小值,则应把AQ与PC转换到一条直线,利用全等三角形可确定∠QBT的位置,连接EF,利用相似三角形可确定T点位置,连接AT交BC于Q,则QT=PC,根据全等三角形确定∠ACP,据此即可得出点P、Q的位置.
(1)AB=![]() =5.
=5.
(2)∵要使AQ+PC有最小值,
∴应把AQ与PC转换到一条直线,即使QT=PC,得AQ+PC=AT,
∴作△BQT≌△APC即可,
∴应作∠CBT=∠BAC,BT=AC=3,
∴连接BD,则∠CBT=∠BAC,
∵BD=5,
∴要使BT=3,则![]() =
=![]() ,
,
∴连接EF,则![]() =
=![]() =
=![]() ,即BT=3,
,即BT=3,
∴连接AT,交BC于Q,则Q点即为所求,
∵△BQT≌△APC,
∴∠BTA=∠ACP,
∴只要作△ABT的全等三角形即可,
∵AC=BT,∠ABT=90°,AB=5,
∴作GA⊥AC,AG=5,则△ABT≌△GAC,
∴连接CG,交AB于P,则∠ACP=∠ATB,则P点即为所求.

故答案为:5;取格点![]() .连接
.连接![]() ,它们相交于点
,它们相交于点![]() ,连接
,连接![]() ,分别交
,分别交![]() 于点
于点![]() ,则线段
,则线段![]() 和
和![]() 即为所求.
即为所求.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
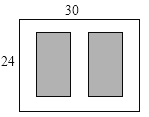
【题目】如图,某小区有一块长为30 m,宽为24 m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480 m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为________m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是菱形ABCD边上的动点,它从点A出发沿A→B→C→D路径匀速运动到点D,设![]() 的面积为y,P点的运动时间为x,则y关于x的函数图象大致为( )
的面积为y,P点的运动时间为x,则y关于x的函数图象大致为( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的进步和网络资源的丰富,在线学习已成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
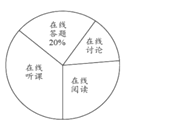
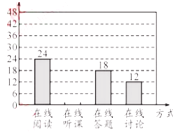
根据图中信息,解答下列问题:
(1)求本次调查的学生总人数,并补全条形统计图;
(2)求扇形统计图中“在线讨论”对应的扇形圆心角的度数;
(3)该校共有学生![]() 人,请你估计该校对在线阅读最感兴趣的学生人数.
人,请你估计该校对在线阅读最感兴趣的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数的学习过程中,我们总会对其中一些具有某种特性的数进行研究,如学习自然数时,我们研究了偶数、奇数、合数、质数等.现在我们来研究一种特殊的自然数﹣“纯数”.
定义:对于自然数n,在通过列竖式进行![]() 的运算时各位都不产生进位现象,则称这个自然数n为“纯数”.
的运算时各位都不产生进位现象,则称这个自然数n为“纯数”.
例如:32是“纯数”,因为![]() 在列竖式计算时各位都不产生进位现象;23不是“纯数”,因为
在列竖式计算时各位都不产生进位现象;23不是“纯数”,因为![]() 在列竖式计算时个位产生了进位.
在列竖式计算时个位产生了进位.
(1)请直接写出1949到2019之间的“纯数”;
(2)求出不大于100的“纯数”的个数,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位要印刷“市民文明出行,遵守交通安全”的宣传材料.甲印刷厂提出:每份材料收1元印刷费,另收150元的制版费;乙印刷厂提出:每份材料收2.5元印刷费,不收制版费.设在同一家印刷厂一次印制数量为![]() 份(
份(![]() 为正整数).
为正整数).
(1)根据题意,填写下表:
一次印制数量(份) | 5 | 10 | 20 | … |
|
甲印刷厂收费(元) | 155 | … | |||
乙印刷厂收费(元) | 12.5 | … |
(2)在印刷品数量大于800份的情况下选哪家印刷厂印制省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最小值和最大值之和是( )
,点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最小值和最大值之和是( )
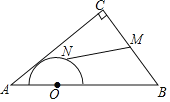
A. 5B. 6C. 7D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() ,点
,点![]() ,与y轴交于点C,且过点
,与y轴交于点C,且过点![]() .点P、Q是抛物线
.点P、Q是抛物线![]() 上的动点.
上的动点.
(1)求抛物线的解析式;
(2)当点P在直线OD下方时,求![]() 面积的最大值.
面积的最大值.
(3)直线OQ与线段BC相交于点E,当![]() 与
与![]() 相似时,求点Q的坐标.
相似时,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
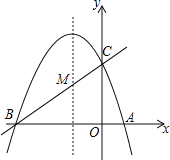
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com