
【题目】在数的学习过程中,我们总会对其中一些具有某种特性的数进行研究,如学习自然数时,我们研究了偶数、奇数、合数、质数等.现在我们来研究一种特殊的自然数﹣“纯数”.
定义:对于自然数n,在通过列竖式进行![]() 的运算时各位都不产生进位现象,则称这个自然数n为“纯数”.
的运算时各位都不产生进位现象,则称这个自然数n为“纯数”.
例如:32是“纯数”,因为![]() 在列竖式计算时各位都不产生进位现象;23不是“纯数”,因为
在列竖式计算时各位都不产生进位现象;23不是“纯数”,因为![]() 在列竖式计算时个位产生了进位.
在列竖式计算时个位产生了进位.
(1)请直接写出1949到2019之间的“纯数”;
(2)求出不大于100的“纯数”的个数,并说明理由.
【答案】(1)2000,2001,2002,2010,2011,2012;(2)0,1,2,10,11,12,20,21,22,30,31,32,100.共13个.
【解析】
(1)根据“纯数”的概念,从2000至2019之间找出“纯数”;
(2)根据“纯数”的概念得到不大于100的数个位不超过2,十位不超过3时,才符合“纯数”的定义解答.
解:(1)显然1949至1999都不是“纯数”,因为在通过列竖式进行![]() 的运算时要产生进位.
的运算时要产生进位.
在2000至2019之间的数,只有个位不超过2时,才符合“纯数”的定义.
所以所求“纯数”为2000,2001,2002,2010,2011,2012;
(2)不大于100的“纯数”的个数有13个,理由如下:
因为个位不超过2,十位不超过3时,才符合“纯数”的定义,
所以不大于100的“纯数”有:0,1,2,10,11,12,20,21,22,30,31,32,100.共13个.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴相交于点
轴相交于点![]() 、
、![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
![]() 求该函数的表达式;
求该函数的表达式;
![]() 点
点![]() 为该函数在第一象限内的图象上一点,过点
为该函数在第一象限内的图象上一点,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() .
.
①求线段![]() 的最大值;
的最大值;
②若以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
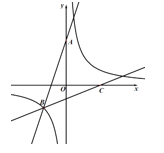
【题目】如下图,在平面直角坐标系中,直线![]() :
:![]() +n与y轴交于点A 与反比例函数
+n与y轴交于点A 与反比例函数![]() 的图象交于B (-2,-2),直线
的图象交于B (-2,-2),直线![]() 过B点与x轴交于点C,OA:OC= 4:3.
过B点与x轴交于点C,OA:OC= 4:3.
(1)求m的值以及直线![]() 的函数表达式;
的函数表达式;
(2)连接AC,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
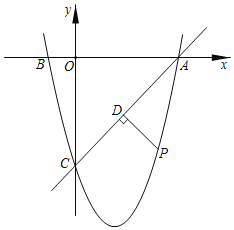
【题目】如图,在平面直角坐标系中,已知点![]() 的坐标为
的坐标为![]() ,且
,且![]() ,抛物线
,抛物线![]() 图象经过
图象经过![]() 三点.
三点.
(1)求![]() 两点的坐标;
两点的坐标;
(2)求抛物线的解析式;
(3)若点![]() 是直线
是直线![]() 下方的抛物线上的一个动点,作
下方的抛物线上的一个动点,作![]() 于点
于点![]() ,当
,当![]() 的值最大时,求此时点
的值最大时,求此时点![]() 的坐标及
的坐标及![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
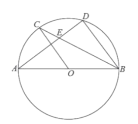
【题目】如图,![]() 为⊙
为⊙![]() 的直径,
的直径,![]() ,
,![]() 为圆上的两点,
为圆上的两点,![]() ,弦
,弦![]() ,
,![]() 相交于点
相交于点![]() ,
,
(1)求证:![]()
(2)若![]() ,
,![]() ,求⊙
,求⊙![]() 的半径;
的半径;
(3)在(2)的条件下,过点![]() 作⊙
作⊙![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 交⊙
交⊙![]() 于
于![]() ,
, ![]() 两点(点
两点(点![]() 在线段
在线段![]() 上),求
上),求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
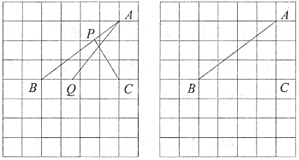
【题目】如图,在由边长都为1的小正方形组成的网格中,点![]() ,
,![]() ,
,![]() 均为格点,点
均为格点,点![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 上的动点,且满足
上的动点,且满足![]() .
.
(1)线段![]() 的长度等于__________;
的长度等于__________;
(2)当线段![]() 取得最小值时,请借助无刻度直尺在给定的网格中画出线段
取得最小值时,请借助无刻度直尺在给定的网格中画出线段![]() 和
和![]() ,并简要说明你是怎么画出点Q,P的:_______________________.
,并简要说明你是怎么画出点Q,P的:_______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
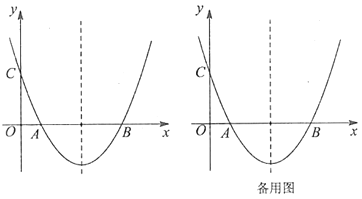
【题目】如图,抛物线![]() 经点
经点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
(1)求抛物线的解析式;
(2)定义:平面上的任一点到二次函数图象上与它横坐标相同的点的距离,称为点到二次函数图象的垂直距离.如:点![]() 到二次函数图象的垂直距离是线段
到二次函数图象的垂直距离是线段![]() 的长.已知点
的长.已知点![]() 为抛物线对称轴上的一点,且在
为抛物线对称轴上的一点,且在![]() 轴上方,点
轴上方,点![]() 为平面内一点,当以
为平面内一点,当以![]() 为顶点的四边形是边长为4的菱形时,请求出点
为顶点的四边形是边长为4的菱形时,请求出点![]() 到二次函数图象的垂直距离.
到二次函数图象的垂直距离.
(3)在(2)中,当点![]() 到二次函数图象的垂直距离最小时,在
到二次函数图象的垂直距离最小时,在![]() 为顶点的菱形内部是否存在点
为顶点的菱形内部是否存在点![]() ,使得
,使得![]() 之和最小,若存在,请求出最小值;若不存在,请说明理由.
之和最小,若存在,请求出最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
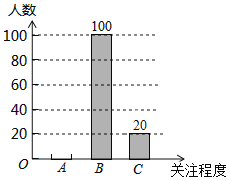
【题目】湖南省作为全国第三批启动高考综合改革的省市之一,从2018年秋季入学的高中一年级学生开始实施高考综合改革.深化高考综合改革,承载着广大考生的美好期盼,事关千家万户的切身利益,社会关注度高.为了了解我市某小区居民对此政策的关注程度,某数学兴趣小组随机采访了该小区部分居民,根据采访情况制做了如统计图表:
关注程度 | 频数 | 频率 |
A.高度关注 | m | 0.4 |
B.一般关注 | 100 | 0.5 |
C.没有关注 | 20 | n |
(1)根据上述统计图表,可得此次采访的人数为 ,m= ,n= .
(2)根据以上信息补全图中的条形统计图.
(3)请估计在该小区1500名居民中,高度关注新高考政策的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.
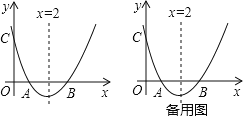
(1)求抛物线的函数表达式;
(2)设D为抛物线的顶点,连接DA、DB,试判断△ABD的形状,并说明理由;
(3)设P为对称轴上一动点,要使PC﹣PB的值最大,求出P点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com