
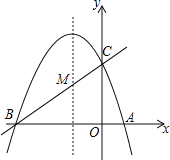
����Ŀ����ͼ����֪������y��ax2+bx+c(a��0)�ĶԳ���Ϊֱ��x����1���������߾���A(1��0)��C(0��3)���㣬��x�ύ�ڵ�B��
(1)��ֱ��y��mx+n����B��C���㣬��ֱ��BC�������ߵĽ���ʽ��
(2)�������ߵĶԳ���x����1����һ��M��ʹ��M����A�ľ����뵽��C�ľ���֮����С�������M�����ꣻ
(3)���PΪ�����ߵĶԳ���x����1�ϵ�һ�����㣬��ʹ��BPCΪֱ�������εĵ�P�����꣮
���𰸡�(1)�����߽���ʽΪy����x2��2x+3��ֱ�ߵĽ���ʽΪy��x+3��(2)����M����A�ľ����뵽��C�ľ���֮����СʱM������Ϊ(��1��2)��(3)P������Ϊ(��1����2)��(��1��4)��(��1��![]() ) ��(��1��
) ��(��1��![]() )��
)��
��������
![]() �Ȱѵ�A��C������ֱ���������߽���ʽ�õ�a��b��c�Ĺ�ϵʽ���ٸ��������ߵĶԳ��᷽�̿ɵ�a��b�Ĺ�ϵ���������õ������飬�ⷽ���飬���a��b��c��ֵ���ɵõ������߽���ʽ����B��C������������ֱ��
�Ȱѵ�A��C������ֱ���������߽���ʽ�õ�a��b��c�Ĺ�ϵʽ���ٸ��������ߵĶԳ��᷽�̿ɵ�a��b�Ĺ�ϵ���������õ������飬�ⷽ���飬���a��b��c��ֵ���ɵõ������߽���ʽ����B��C������������ֱ��![]() ���ⷽ�������m��n��ֵ���ɵõ�ֱ�߽���ʽ��
���ⷽ�������m��n��ֵ���ɵõ�ֱ�߽���ʽ��
![]() ��ֱ��BC��Գ���
��ֱ��BC��Գ���![]() �Ľ���ΪM�����ʱ
�Ľ���ΪM�����ʱ![]() ��ֵ��С
��ֵ��С![]() ��
��![]() ����ֱ��
����ֱ��![]() ��y��ֵ�����������M���ꣻ
��y��ֵ�����������M���ꣻ
![]() ��
��![]() ������Ϊ
������Ϊ![]() ��
��![]() �����Կɵ�
�����Կɵ�![]() ��
��![]() ��
��![]() ���ٷ���������ֱ����������������tֵ���������P�����꣮
���ٷ���������ֱ����������������tֵ���������P�����꣮
�⣺(1)������ã� ��
��
��֮�ã� ��
��
�������߽���ʽΪy����x2��2x+3
���Գ���Ϊx����1���������߾���A(1��0)��
����B(��3��0)��C(0��3)�ֱ����ֱ��y��mx+n��
��![]() ��
��
��֮�ã�![]() ��
��
��ֱ��y��mx+n�Ľ���ʽΪy��x+3��
(2)��ֱ��BC��Գ���x����1�Ľ���ΪM�����ʱMA+MC��ֵ��С��
��x����1����ֱ��y��x+3�ã�y��2��
��M(��1��2)��
������M����A�ľ����뵽��C�ľ���֮����СʱM������Ϊ(��1��2)��
(3)��P(��1��t)��
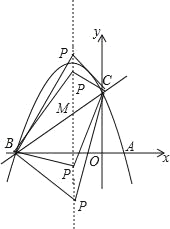
����B(��3��0)��C(0��3)��
��BC2��18��PB2��(��1+3)2+t2��4+t2��PC2��(��1)2+(t��3)2��t2��6t+10��
������BΪֱ�Ƕ��㣬��BC2+PB2��PC2����18+4+t2��t2��6t+10��֮�ã�t����2��
������CΪֱ�Ƕ��㣬��BC2+PC2��PB2����18+t2��6t+10��4+t2��֮�ã�t��4��
������PΪֱ�Ƕ��㣬��PB2+PC2��BC2����4+t2+t2��6t+10��18��֮�ã�t1��![]() ��t2��
��t2��![]() ��
��
��������P������Ϊ(��1����2)��(��1��4)��(��1��![]() ) ��(��1��
) ��(��1��![]() )��
)��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
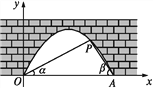
����Ŀ����ͼ������������,P����һ������,ˮ��OA��4 m,��O,A�����۲�P��,���Ƿֱ�Ϊ��,��,��tan ��=![]() ,tan ��=
,tan ��=![]() ,��OΪԭ��,OA����ֱ��Ϊx�Ὠ��ƽ��ֱ������ϵ.
,��OΪԭ��,OA����ֱ��Ϊx�Ὠ��ƽ��ֱ������ϵ.
(1)���P������.
(2)ˮ������1 m,ˮ�������?(�����ȷ��0.1 m.�ο�����: ![]() ��1.41)
��1.41)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
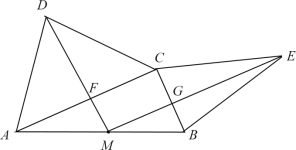
����Ŀ����ͼ����Rt��ABC�У���ACB��90�����ֱ���ACBCΪ�ױߣ�����ABC�ⲿ��������ADC����CEB����MΪAB�е㣬����MDME�ֱ���ACBC���ڵ�F�͵�G��
��֤�ı���MFCG�Ǿ��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����DE��x���y��ֱ��ڵ�D��3��0���͵�E��0��4��������C�ӵ�M��5��0����������1����λ����/����ٶ���x�������������˶������ͬʱ������P�ӵ�D������Ҳ��1����λ����/����ٶ�������DE�ķ����������˶������˶�ʱ��Ϊt�룬

��1�����ú�t�Ĵ���ʽ�ֱ��ʾ����C���P�����ꣻ
��2���Ե�CΪ���ģ�![]() ����λ����Ϊ�뾶����C��x�ύ��A��B���㣨��A�ڵ�B����ࣩ������PA��PB��
����λ����Ϊ�뾶����C��x�ύ��A��B���㣨��A�ڵ�B����ࣩ������PA��PB��
������C������DE�й�����ʱ����t��ȡֵ��Χ��
������PABΪ����������ʱ����t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
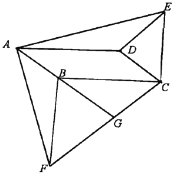
����Ŀ����ͼ������ABCD�У��ֱ��Ա�BC��CD��������BCF����CDE��ʹBC=BF��CD=DE����CBF����CDE������AF��AE.
��1����֤����ABF�ա�EDA��
��2���ӳ�AB��CF�ཻ��G����AF��AE����֤BF��BC.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУѡ��һ����ѧ���μ�������ˮ�������ɱ�������ҪΪÿλ����ѧ������һ��ñ�ӣ��̳��涨����һ���Թ���200����200�����ϣ��ɰ������۸������200������ֻ�ܰ����ۼ۸�����Ϊÿλ����ѧ������1������ôֻ�ܰ����ۼ۸������900Ԫ��������45������ô���������۸��ͬ������900Ԫ���ʣ�
��1������ѧ������x��ʲô��Χ�ڣ�
��2�����������۹���15���밴���ۼ۹���12���Ŀ���ͬ����ô����ѧ������x�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ���˽�ѧ�����Ĵ�ŵ�����(�����μǡ����������塷��ˮ䰴�������¥�Ρ�)���Ķ�����������Ĵ�ŵ�����������˼�������������ȫУѧ���н����˳������飮���ݵ��������Ƴ�����ʾ��������������ͳ��ͼ������ͼ����Ϣ����������⣺
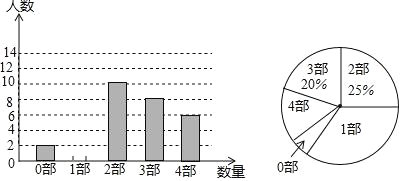
(1)���ε���һ����ȡ��_____��ѧ��������ͳ��ͼ����4�����������ε�Բ�Ľ�Ϊ____�ȣ�
(2)�벹ȫ����ͳ��ͼ��������ѧ��2000��ѧ��������������Ķ�1���Ĵ�ŵ�������ѧ���ж�������
(3)û�ж����Ĵ�����������ѧ�������Ĵ�ŵ������и������ѡ��һ�����Ķ��������б�������״ͼ������ѡ��ͬһ�����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1�����ı���ABCD�ı�BC���ӳ�����ȡһ��E����ֱ��BC��ͬ����һ����CEΪ�ĵ�����CEF���������B+��F��180�������������CEFΪ�ı���ABCD������������������
��1����ͼ1������CEF��������ABCD������������������
������AC�����ACF���� ����
����CE��2BC������AE��CF��H����֤��H��CF���е㣻
��2����ͼ2������CEF������ABCD��������������������B��60����M���߶�AE���е㣬����DM��FM�����벢֤��DM��FM��λ����������ϵ��
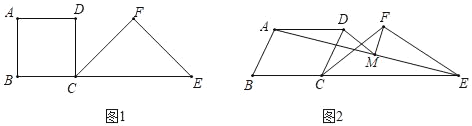
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���B��60����AB��2��������ABCD��BC���е�E˳ʱ����ת60���õ�����A'B'C'D'�����е�D���˶�·��Ϊ![]() ����ͼ����Ӱ���ֵ����Ϊ__��
����ͼ����Ӱ���ֵ����Ϊ__��
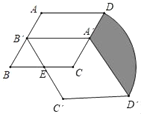
![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com