
【题目】某校选派一部分学生参加“六盘水市马拉松比赛”,要为每位参赛学生购买一顶帽子.商场规定:凡一次性购买200顶或200顶以上,可按批发价付款;购买200顶以下只能按零售价付款.如果为每位参赛学生购买1顶,那么只能按零售价付款,需用900元;如果多购买45顶,那么可以按批发价付款,同样需用900元.问:
(1)参赛学生人数x在什么范围内?
(2)若按批发价购买15顶与按零售价购买12顶的款相同,那么参赛学生人数x是多少?
【答案】(1)参赛学生人数在155≤x<200范围内;
(2)参赛学生人数是180人.
【解析】
试题(1)设参赛学生人数有x人,根据每位参赛学生购买1顶,只能按零售价付款,需用900元,如果多购买45顶,那么可以按批发价付款,同样需用900元,列出不等式,求解即可;
(2)根据参赛学生为x人和按批发价购买15顶与按零售价购买12顶的款相同,列出方程,求出方程的解即可.
试题解析:(1)设参赛学生人数有x人,
由题意得,x<200且x+45≥200,
解得:155≤x<200;
答:参赛学生人数在155≤x<200范围内;
(2)根据题意得:
![]() +12=
+12=![]() +15,
+15,
解得:x=180,
经检验x=180是原方程的解.
答:参赛学生人数是180人.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(cm2).
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是的直径,PA与⊙O 相切于点A,点C在⊙O 上,且PC=PA,
(1)求证PC是⊙O的切线;
(2)过点C作CD⊥AB于点E,交⊙O于点D,若CD=PA=2![]() ,
,
①求图中阴影部分面积;
②连接AC,若△PAC的内切圆圆心为I,则线段IE的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
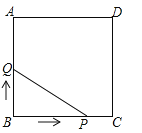
【题目】(3分)如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
A.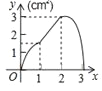 B.
B.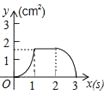 C.
C.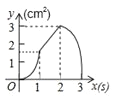 D.
D.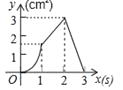
查看答案和解析>>
科目:初中数学 来源: 题型:
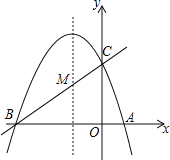
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
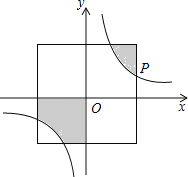
【题目】如图,在直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(3a,a)是反比例函数![]() (k>0)的图象上与正方形的一个交点.若图中阴影部分的面积等于9,则这个反比例函数的解析式为 ▲ .
(k>0)的图象上与正方形的一个交点.若图中阴影部分的面积等于9,则这个反比例函数的解析式为 ▲ .
查看答案和解析>>
科目:初中数学 来源: 题型:
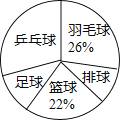
【题目】某中学为了了解学生最喜欢的一种球类运动,以便合理安排活动场地,在全校至少喜欢一种球类(乒乓球、羽毛球、排球、篮球、足球)运动的1800名学生中,随机抽取了若干名学生进行调查(每人只能在这五种球类运动中选择一种),调查结果统计如下:
球类名称 | 乒乓球 | 羽毛球 | 排球 | 篮球 | 足球 |
人数 | 42 | a | b | 33 | 21 |
解答下列问题:
(1)这次抽样调查的总人数是 ,统计表中a的值为 .
(2)求扇形统计图中排球一项的扇形圆心角度数.
(3)试估计全校1800名学生中最喜欢乒乓球运动的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
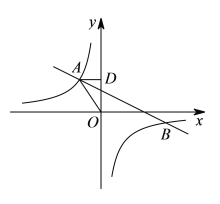
【题目】如图,在平面直角坐标系中,反比例函数![]()
![]() 与一次函数
与一次函数![]() 交于第二、四象限的
交于第二、四象限的![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求反比例函数和一次函数的解析式;
(2)请根据图象直接写出![]() 的自变量
的自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com