
【题目】如图,在⊙O中,AB是的直径,PA与⊙O 相切于点A,点C在⊙O 上,且PC=PA,
(1)求证PC是⊙O的切线;
(2)过点C作CD⊥AB于点E,交⊙O于点D,若CD=PA=2![]() ,
,
①求图中阴影部分面积;
②连接AC,若△PAC的内切圆圆心为I,则线段IE的长为 .

【答案】(1)详见解析;(2)①S阴影=![]() . ②
. ②![]() .
.
【解析】
(1)连接OCOP,证明△PCO≌△PAO,即可解答
(2)①作CM⊥AP于点M,得到△PCA是等边三角形.然后在Rt△COE中得到OC=2.即可解答 .
②根据题意求出CH=![]() AH=3,由I为正△PAC的内心,即可求出解答 .
AH=3,由I为正△PAC的内心,即可求出解答 .
(1)证明:连接OCOP,
∵点C在⊙O上,
∴OC为半径.
∵PA与⊙O相切于点A,
∴OA⊥PA.
∴∠PAO=90°.
∵OC=OA,
OP=OP,
PC=PA,
∴△PCO≌△PAO.
∴∠PCO=∠PAO=90°.
∴PC⊥OC.
∴PC是⊙O的切线.
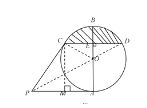
(2)①作CM⊥AP于点M,
∵CD⊥AB,
∴CE=DE=![]() ,∠CEA=90°.
,∠CEA=90°.
∴四边形CMAE是矩形.
∴AM=![]() .
.
∴PM=AM.
∴PC=AC.
∵PC=PA,
∴△PCA是等边三角形.
∴∠PAC=60°.
∴∠CAB=30°.
∴∠COE=60°.
∴∠COD=120°.
在Rt△COE中,
sin60°=![]() ,
,
∴OC=2.
∴S阴影=![]() π-
π-![]() .
.
②∵AP=2![]() ,AH=CE=
,AH=CE=![]()
∴CH=![]() AH=3
AH=3
又∵I为正△PAC的内心
∴CI=![]() CH=2
CH=2
∴IE=![]() =
=![]() =
=![]()


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
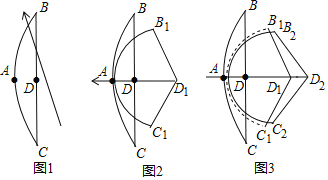
【题目】如图1是小明制作的一副弓箭,点A,D分别是弓臂BAC与弓弦BC的中点,弓弦BC=60cm.沿AD方向拉动弓弦的过程中,假设弓臂BAC始终保持圆弧形,弓弦不伸长.如图2,当弓箭从自然状态的点D拉到点D1时,有AD1=30cm,∠B1D1C1=120°.
(1)图2中,弓臂两端B1,C1的距离为______cm.
(2)如图3,将弓箭继续拉到点D2,使弓臂B2AC2为半圆,则D1D2的长为____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
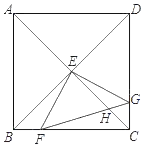
【题目】如图,正方形ABCD的边长为![]() ,对角线AC和BD交于点E,点F是BC边上一动点(不与点B,C重合),过点E作EF的垂线交CD于点G,连接FG交EC于点H.设BF=x,CH=y,则y与x的函数关系的图象大致是( )
,对角线AC和BD交于点E,点F是BC边上一动点(不与点B,C重合),过点E作EF的垂线交CD于点G,连接FG交EC于点H.设BF=x,CH=y,则y与x的函数关系的图象大致是( )
A. 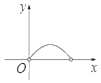 B.
B. 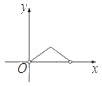 C.
C. 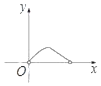 D.
D. 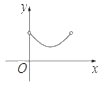
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了庆祝“五四”青年节,我市某中学举行了书法比赛,赛后随机抽查部分参赛同学成绩(满分为100分),并制作成图表如下
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x≤100 | 20 | 0.1 |
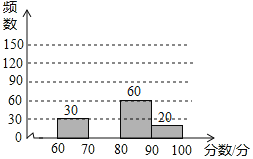
请根据以上图表提供的信息,解答下列问题:
(1)这次随机抽查了 名学生;表中的数m= ,n= ;
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是 ;
(4)全校共有600名学生参加比赛,估计该校成绩不低于80分的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
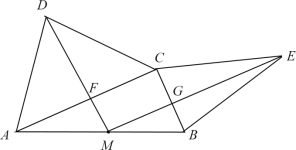
【题目】如图,在Rt△ABC中,∠ACB=90°,分别以ACBC为底边,向△ABC外部作等腰△ADC和△CEB,点M为AB中点,连接MDME分别与ACBC交于点F和点G.
求证四边形MFCG是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组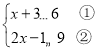 .请结合题意填空,完成本题的解答
.请结合题意填空,完成本题的解答
(Ⅰ)解不等式①,得__________;
(Ⅱ)解不等式②,得__________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:

(Ⅳ)原不等式组的解集为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知射线DE与x轴和y轴分别交于点D(3,0)和点E(0,4).动点C从点M(5,0)出发,以1个单位长度/秒的速度沿x轴向左作匀速运动,与此同时,动点P从点D出发,也以1个单位长度/秒的速度沿射线DE的方向作匀速运动,设运动时间为t秒,

(1)请用含t的代数式分别表示出点C与点P的坐标;
(2)以点C为中心,![]() 个单位长度为半径的⊙C与x轴交于A、B两点(点A在点B的左侧),连接PA、PB.
个单位长度为半径的⊙C与x轴交于A、B两点(点A在点B的左侧),连接PA、PB.
①当⊙C与射线DE有公共点时,求t的取值范围;
②当△PAB为等腰三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校选派一部分学生参加“六盘水市马拉松比赛”,要为每位参赛学生购买一顶帽子.商场规定:凡一次性购买200顶或200顶以上,可按批发价付款;购买200顶以下只能按零售价付款.如果为每位参赛学生购买1顶,那么只能按零售价付款,需用900元;如果多购买45顶,那么可以按批发价付款,同样需用900元.问:
(1)参赛学生人数x在什么范围内?
(2)若按批发价购买15顶与按零售价购买12顶的款相同,那么参赛学生人数x是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,Rt△OCD的一边OC在x轴上,∠OCD=90°,点D在第一象限,OC=6,DC=4,反比例函数的图象经过OD的中点A.
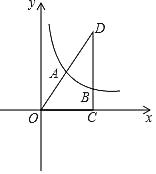
(1)求该反比例函数的解析式;
(2)若该反比例函数的图象与Rt△OCD的另一边DC交于点B,求过A、B两点的直线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com