
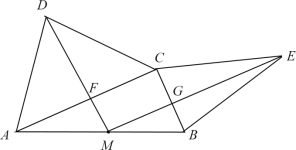
【题目】如图,在Rt△ABC中,∠ACB=90°,分别以ACBC为底边,向△ABC外部作等腰△ADC和△CEB,点M为AB中点,连接MDME分别与ACBC交于点F和点G.
求证四边形MFCG是矩形.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
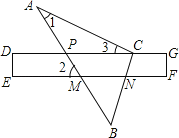
【题目】如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,
(1)作出△APC的PC边上的高;
(2)若∠2=51°,求∠3;
(3)若直尺上点P处刻度为2,点C处为8,点M处为3,点N处为7,求S△BMN:S△BPC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
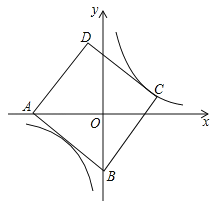
【题目】如图,正方形ABCD的边长为5,点A的坐标为(﹣4,0),点B在y轴上,若反比例函数![]() (k≠0)的图象过点C,则该反比例函数的表达式为( )
(k≠0)的图象过点C,则该反比例函数的表达式为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世界500强H公司决定购买某演唱会门票奖励部分优秀员工,演唱会的购票方式有以下两种,
方式一:若单位赞助广告费10万元,则该单位所购门票的价格为每张0.02万元(其中总费用=广告赞助费+门票费);
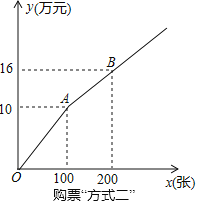
方式二:如图所示,设购买门票x张,总费用为y万元
(1)求用购票“方式一”时y与x的函数关系式;
(2)若H、A两家公司分别釆用方式一、方式二购买本场演唱会门票共400张,且A公司购买超过100张,两公司共花费27.2万元,求H、A两公司各购买门票多少张?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是的直径,PA与⊙O 相切于点A,点C在⊙O 上,且PC=PA,
(1)求证PC是⊙O的切线;
(2)过点C作CD⊥AB于点E,交⊙O于点D,若CD=PA=2![]() ,
,
①求图中阴影部分面积;
②连接AC,若△PAC的内切圆圆心为I,则线段IE的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从![]() 地到
地到![]() 地的公路需经过
地的公路需经过![]() 地,图中
地,图中![]() ,
,![]() ,
,![]() ,因城市规划的需要,将在
,因城市规划的需要,将在![]() 两地之间修建一条笔直的公路.
两地之间修建一条笔直的公路.
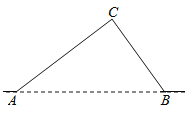
(Ⅰ)求改直的公路![]() 的长;
的长;
(Ⅱ)问公路改直后比原来缩短了多少![]() ?(参考数据:
?(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() 取
取![]() .)(结果保留小数点后一位).
.)(结果保留小数点后一位).
查看答案和解析>>
科目:初中数学 来源: 题型:
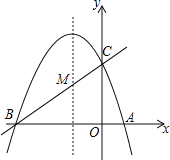
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com